题目内容
4.如图,长方形纸片ABCD中,AB=8,将纸片折叠,使顶点B落在边AD上的E点处,折痕的一端G点在边BC上.(1)如图(1),当折痕的另一端F在AB边上且AE=4时,求AF的长
(2)如图(2),当折痕的另一端F在AD边上且BG=10时,
①求证:EF=EG.
②求AF的长.

分析 (1)根据翻折的性质可得BF=EF,然后用AF表示出EF,在Rt△AEF中,利用勾股定理列出方程求解即可;
(2)①根据翻折的性质可得∠BGF=∠EGF,再根据两直线平行,内错角相等可得∠BGF=∠EFG,从而得到∠EGF=∠EFG,再根据等角对等边证明即可;
②根据翻折的性质可得EG=BG,HE=AB,FH=AF,然后在Rt△EFH中,利用勾股定理列式计算即可得解.
解答  (1)解:如图1,∵纸片折叠后顶点B落在边AD上的E点处,
(1)解:如图1,∵纸片折叠后顶点B落在边AD上的E点处,
∴BF=EF,
∵AB=8,
∴EF=8-AF,
在Rt△AEF中,AE2+AF2=EF2,
即42+AF2=(8-AF)2,
解得AF=3;
(2)如图2,
①证明:∵纸片折叠后顶点B落在边AD上的E点处,
∴∠BGF=∠EGF,
∵长方形纸片ABCD的边AD∥BC,
∴∠BGF=∠EFG,
∴∠EGF=∠EFG,
∴EF=EG;
②解:∵纸片折叠后顶点B落在边AD上的E点处,
∴EG=BG=10,HE=AB=8,FH=AF,
∴EF=EG=10,
在Rt△EFH中,FH=$\sqrt{E{F}^{2}-H{E}^{2}}$=$\sqrt{1{0}^{2}-{8}^{2}}$=6,
∴AF=FH=6.
点评 本题考查了翻折变换的性质,勾股定理的应用,相似三角形的判定与性质,熟记翻折前后两个图形能够重合得到相等的线段和角是解题的关键.

练习册系列答案
相关题目
14.在平面直角坐标系中,⊙O的半径为5,圆心O为坐标原点,则点P(3,-4)与⊙O的位置关系是( )
| A. | 点P在⊙O上 | B. | 点P在⊙O外部 | C. | 点P在⊙O内部 | D. | 不能确定 |
15.我省从2010年7月开始实施阶梯电价制,居民生活用电价格方案如下表:
例:若某用户2010年8月份的用电量为300度,则需缴交电费为:200×0.5+(300-200)×0.55=155(元).
(1)填空:如果小华家2010年9月份的用电量为100度,则需缴交电费50元;
(2)如果小华家2010年10月份的用电量为a度(其中200<a≤400),则需缴交电费多少元?(用含a的代数式表示,并化简)
(3)如果小华家2010年11、12两个月共用电700度(其中12月份的用电量达到“第3档”),设11月份的用电量为b度,则小华家这两个月共需缴交电费多少元?(用含b的代数式表示,并化简)
| 档次 | 月用电量 | 电价(单位:元/度) |
| 第1档 | 月用电量≤200度 | 0.5 |
| 第2档 | 200度<月用电量≤400度 | 0.55 |
| 第3档 | 月用电量>400度 | 0.8 |
(1)填空:如果小华家2010年9月份的用电量为100度,则需缴交电费50元;
(2)如果小华家2010年10月份的用电量为a度(其中200<a≤400),则需缴交电费多少元?(用含a的代数式表示,并化简)
(3)如果小华家2010年11、12两个月共用电700度(其中12月份的用电量达到“第3档”),设11月份的用电量为b度,则小华家这两个月共需缴交电费多少元?(用含b的代数式表示,并化简)
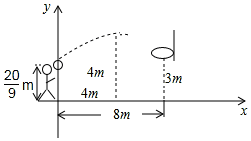 小明跳起投篮,球出手时离地面$\frac{20}{9}$m,球出手后在空中沿抛物线路径运动,并在距出手点水平距离4m处达到最高4m.已知篮筐中心距地面3m,与球出手时的水平距离为8m,建立如图所示的平面直角坐标系.
小明跳起投篮,球出手时离地面$\frac{20}{9}$m,球出手后在空中沿抛物线路径运动,并在距出手点水平距离4m处达到最高4m.已知篮筐中心距地面3m,与球出手时的水平距离为8m,建立如图所示的平面直角坐标系.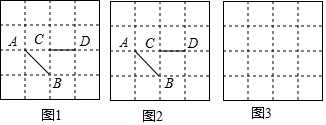
 如图,已知面积为1的四边形ABCD内接于⊙O,AC⊥BD,则四边形OABC的面积为$\frac{1}{2}$.
如图,已知面积为1的四边形ABCD内接于⊙O,AC⊥BD,则四边形OABC的面积为$\frac{1}{2}$.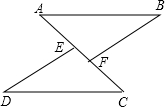 如图,在△ABF与△CDE中,AB=CD,BF=DE,点A、E、F、C在同一条直线上,AE=CF,求证:AB∥CD.
如图,在△ABF与△CDE中,AB=CD,BF=DE,点A、E、F、C在同一条直线上,AE=CF,求证:AB∥CD.