题目内容
2.下列说法正确的个数是( )①-4没有立方根;②-5的立方根是-$\root{3}{-5}$;③1的立方根是±1;④$\frac{1}{36}$的立方根是$\frac{1}{6}$;⑤64的立方根是4.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据正数的立方根是正数,负数的立方根是负数,可以求出题目中各式子的结果,然后与题目中的结果对比,即可判断哪个是正确的,哪个是错误的,本题得以解决.
解答 解:∵正数的立方根是正数,负数的立方根是负数,
∴-4有立方根,故①错误;
-5的立方根是$\root{3}{-5}$,故②错误;
$\root{3}{1}=1$,故③错误;
$\frac{1}{36}$的立方根是$\root{3}{\frac{1}{36}}$,故④错误;
$\root{3}{64}=4$,故⑤正确;
故选A.
点评 本题考查立方根,解题的关键是明确正数的立方根是正数,负数的立方根是负数.

练习册系列答案
相关题目
17.已知|x+y-3|+(x-2y)2=0,则( )
| A. | $\left\{\begin{array}{l}{x=-1}\\{y=-2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=-2}\\{y=-1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$ |
14.两条直线相交所成的四个角都相等时,这两条直线的位置关系是( )
| A. | 平行 | B. | 相交 | C. | 垂直 | D. | 不能确定 |
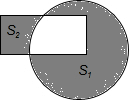 如图,在半径为4的圆中,阴影部分图形的面积为S1;在边长为4,2的矩形中,阴影部分的面积为S2,则S1-S2的值为16π-8.(结果保留π)
如图,在半径为4的圆中,阴影部分图形的面积为S1;在边长为4,2的矩形中,阴影部分的面积为S2,则S1-S2的值为16π-8.(结果保留π)