题目内容
7.已知x2-y2=12,x-y=4,则x+y=3.分析 运用平方差公式可得x2-y2=(x+y)(x-y),代入所给式子的值可得出x+y的值.
解答 解:由题意得:x2-y2=(x+y)(x-y),
∵x2-y2=12,x-y=4,
∴x+y=3.
故答案为:3.
点评 本题考查了平方差公式,解答本题的关键是掌握平方差公式的形式,这是需要我们熟练记忆的内容.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
2.下列说法正确的个数是( )
①-4没有立方根;②-5的立方根是-$\root{3}{-5}$;③1的立方根是±1;④$\frac{1}{36}$的立方根是$\frac{1}{6}$;⑤64的立方根是4.
①-4没有立方根;②-5的立方根是-$\root{3}{-5}$;③1的立方根是±1;④$\frac{1}{36}$的立方根是$\frac{1}{6}$;⑤64的立方根是4.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
19.化简$\frac{1}{3-2\sqrt{2}}$结果正确的是( )
| A. | 3$+2\sqrt{2}$ | B. | 3$-\sqrt{2}$ | C. | 17$+12\sqrt{2}$ | D. | 17-12$\sqrt{2}$ |
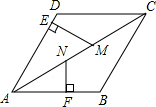 如图,在菱形ABCD中,点M、N在AC上,ME⊥AD,NF⊥AB,若NF=NM=2,ME=3,则AM=6.
如图,在菱形ABCD中,点M、N在AC上,ME⊥AD,NF⊥AB,若NF=NM=2,ME=3,则AM=6. 如图,在△ABC中,AD为∠BAC的平分线,过D作DE∥AB,交AC于E点,在AB上取BF=AE,求证:FE∥BC.
如图,在△ABC中,AD为∠BAC的平分线,过D作DE∥AB,交AC于E点,在AB上取BF=AE,求证:FE∥BC.
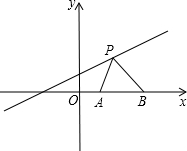 已知如图,点A(1,0),点B(2,0),点P是直线y=$\frac{1}{2}$x+1上的一个动点,PA2+PB2的最小值=$\frac{27}{5}$.
已知如图,点A(1,0),点B(2,0),点P是直线y=$\frac{1}{2}$x+1上的一个动点,PA2+PB2的最小值=$\frac{27}{5}$.