题目内容
12.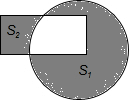 如图,在半径为4的圆中,阴影部分图形的面积为S1;在边长为4,2的矩形中,阴影部分的面积为S2,则S1-S2的值为16π-8.(结果保留π)
如图,在半径为4的圆中,阴影部分图形的面积为S1;在边长为4,2的矩形中,阴影部分的面积为S2,则S1-S2的值为16π-8.(结果保留π)
分析 设两图形重合部分的面积为S3,用含S3的代数式表示出来S1和S2,两者做差即可得出结论.
解答 解:设二者重合部分的面积为S3,
根据题意则有:S1=πr2-S3=16π-S3,
S2=4×2-S3=8-S3,
S1-S2=(16π-S3)-(8-S3)=16π-S3-8+S3=16π-8.
故答案为:16π-8.
点评 本题考查了整式的加减法,解题的关键是用含S3的代数式表示出来S1和S2.本题属于基础题,解决该题型题目时,只要设出重合的量,利用整式加减运算的法则即可得出结论.

练习册系列答案
 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
3.下列说法正确的是( )
| A. | 一组数据:4、1、3、1、2的中位数是3 | |
| B. | 了解一批节能灯的使用寿命,适合用普查的方式 | |
| C. | “明天降雨的概率为$\frac{1}{2}$”,表示明天有半天都在降雨 | |
| D. | 甲、乙两人在相同条件下各射击20次,他们的成绩平均数相同,方差分别是S甲2=0.4.S乙2=0.6,则甲的射击成绩较稳定 |
7.若等腰三角形的一个内角是40°,则它的顶角是( )
| A. | 100° | B. | 40° | C. | 100°或40° | D. | 60° |
4.2015年秋,由于环境污染严重,我国多地出现持续雾霾,某工厂看到商机,加急研发一种专用口罩,工厂接到订单生产高、中、低档专用型口罩共2400个,厂方计划由20个工人一天内加工完成,并要求每人只加工一种类型口罩,根据下表提供的信息,解答下列问题:
(1)若工厂安排3人加工高档口罩、2人加工中档口罩和安排2人加工高档口罩、3人加工中档口罩均获利4800元,请求a、b的值;
(2)①设加工高档口罩的人数为x,加工中档口罩的人数为y,求y与x之间的函数关系式;
②如果加工每种类型口罩的人数均不少于3人,那么加工口罩的人数安排方案有几种?并写出每种安排方案;
③要使此次加工口罩的利润最大,应采用②中哪种方案?并求出最大利润.
| 口罩种类 | 高档 | 中档 | 低挡 |
| 每人可加工口罩的数量(个) | 160 | 120 | 100 |
| 每个口罩获利(元) | a | b | 5 |
(2)①设加工高档口罩的人数为x,加工中档口罩的人数为y,求y与x之间的函数关系式;
②如果加工每种类型口罩的人数均不少于3人,那么加工口罩的人数安排方案有几种?并写出每种安排方案;
③要使此次加工口罩的利润最大,应采用②中哪种方案?并求出最大利润.
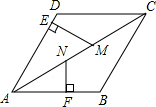 如图,在菱形ABCD中,点M、N在AC上,ME⊥AD,NF⊥AB,若NF=NM=2,ME=3,则AM=6.
如图,在菱形ABCD中,点M、N在AC上,ME⊥AD,NF⊥AB,若NF=NM=2,ME=3,则AM=6.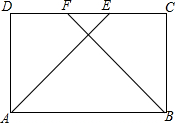 四边形ABCD中,AB∥CD,AB=CD,AE为∠A的平分线,BF为∠B的平分线,E、F在CD上,AE=BF,证明:四边形ABCD是矩形.
四边形ABCD中,AB∥CD,AB=CD,AE为∠A的平分线,BF为∠B的平分线,E、F在CD上,AE=BF,证明:四边形ABCD是矩形.