题目内容
14.在△ABC中,∠A=75°,cosB=$\frac{\sqrt{2}}{2}$,则tanC=$\sqrt{3}$.分析 根据特殊角的三角函数值求出∠B,根据三角形内角和定理求出∠C,利用特殊角的三角函数值解答即可.
解答 解:∵cosB=$\frac{\sqrt{2}}{2}$,
∴∠B=45°,
∴∠C=180°-∠A-∠B=60°,
∴tanC=tan60°=$\sqrt{3}$,
故答案为:$\sqrt{3}$.
点评 本题考查的是特殊角的三角函数值的计算和三角形内角和定理的应用,熟记特殊角的三角函数值是解题的关键.

练习册系列答案
相关题目
4.2015年秋,由于环境污染严重,我国多地出现持续雾霾,某工厂看到商机,加急研发一种专用口罩,工厂接到订单生产高、中、低档专用型口罩共2400个,厂方计划由20个工人一天内加工完成,并要求每人只加工一种类型口罩,根据下表提供的信息,解答下列问题:
(1)若工厂安排3人加工高档口罩、2人加工中档口罩和安排2人加工高档口罩、3人加工中档口罩均获利4800元,请求a、b的值;
(2)①设加工高档口罩的人数为x,加工中档口罩的人数为y,求y与x之间的函数关系式;
②如果加工每种类型口罩的人数均不少于3人,那么加工口罩的人数安排方案有几种?并写出每种安排方案;
③要使此次加工口罩的利润最大,应采用②中哪种方案?并求出最大利润.
| 口罩种类 | 高档 | 中档 | 低挡 |
| 每人可加工口罩的数量(个) | 160 | 120 | 100 |
| 每个口罩获利(元) | a | b | 5 |
(2)①设加工高档口罩的人数为x,加工中档口罩的人数为y,求y与x之间的函数关系式;
②如果加工每种类型口罩的人数均不少于3人,那么加工口罩的人数安排方案有几种?并写出每种安排方案;
③要使此次加工口罩的利润最大,应采用②中哪种方案?并求出最大利润.
2.下列说法正确的个数是( )
①-4没有立方根;②-5的立方根是-$\root{3}{-5}$;③1的立方根是±1;④$\frac{1}{36}$的立方根是$\frac{1}{6}$;⑤64的立方根是4.
①-4没有立方根;②-5的立方根是-$\root{3}{-5}$;③1的立方根是±1;④$\frac{1}{36}$的立方根是$\frac{1}{6}$;⑤64的立方根是4.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
9.水果商贩小李去水果批发市场采购被誉为“果中之王”的泰顺猕猴桃,他了解到猕猴桃有精品盒与普通盒两种包装,精品盒的批发价格每盒60元,普通盒的批发价格每盒40元,现小李购得精品盒与普通盒共60盒,费用共为3100元.
(1)问小李分别购买精品盒与普通盒多少盒?
(2)小李经营着甲、乙两家店铺,每家店铺每天部能售出精品盒与普通盒共30盒,并且每售出一盒精品盒与普通盒,在甲店获利分别为30元和40元,在乙店获利分别为24元和35元.现在小李要将购进的60盒弥猴桃分配给每个店铺各30盒,设分配给甲店精品盒a盒,请你根据题意填写下表:
小李希望在甲店获利不少于1000元的前提下,使自己获取的总利润W最大,应该如何分配?最大的总利润是多少?
(1)问小李分别购买精品盒与普通盒多少盒?
(2)小李经营着甲、乙两家店铺,每家店铺每天部能售出精品盒与普通盒共30盒,并且每售出一盒精品盒与普通盒,在甲店获利分别为30元和40元,在乙店获利分别为24元和35元.现在小李要将购进的60盒弥猴桃分配给每个店铺各30盒,设分配给甲店精品盒a盒,请你根据题意填写下表:
| 精品盒数量(盒) | 普通盒数量(盒) | 合计(盒) | |
| 甲店 | a | 30-a | 30 |
| 乙店 | 35-a | a-5 | 30 |
5. 如图,在方格纸上,△ABC经过变换得到△DEF,下列对变换过程的叙述正确的是( )
如图,在方格纸上,△ABC经过变换得到△DEF,下列对变换过程的叙述正确的是( )
 如图,在方格纸上,△ABC经过变换得到△DEF,下列对变换过程的叙述正确的是( )
如图,在方格纸上,△ABC经过变换得到△DEF,下列对变换过程的叙述正确的是( )| A. | △ABC绕着点A顺时针旋转90°,再向右平移7格 | |
| B. | △ABC向右平移4格,再向上平移7格 | |
| C. | △ABC绕着点A逆时针旋转90°,再向右平移7格 | |
| D. | △ABC向右平移4格,再绕着点B逆时针旋转90° |
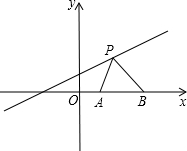 已知如图,点A(1,0),点B(2,0),点P是直线y=$\frac{1}{2}$x+1上的一个动点,PA2+PB2的最小值=$\frac{27}{5}$.
已知如图,点A(1,0),点B(2,0),点P是直线y=$\frac{1}{2}$x+1上的一个动点,PA2+PB2的最小值=$\frac{27}{5}$.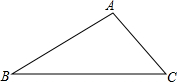 已知:在△ABC中,∠B=45°,∠C=30°,AC=2.求:
已知:在△ABC中,∠B=45°,∠C=30°,AC=2.求: