题目内容
11.计算下面各组算式.(1)$\sqrt{4}×\sqrt{9}$与$\sqrt{4×9}$;
(2)$\sqrt{16}×\sqrt{25}$与$\sqrt{16×25}$;
(3)$\sqrt{0.01}×\sqrt{0.04}$与$\sqrt{0.01×0.04}$;
(4)$\sqrt{\frac{1}{4}}×\sqrt{\frac{16}{9}}$与$\sqrt{\frac{1}{4}×\frac{16}{9}}$
观察每组之间有什么关系?并把这个规律用式子总结出来.
分析 先把前面的式子算出结果,然后观察其中的规律,写出来即可.
解答 解:(1)$\sqrt{4}×\sqrt{9}=2×3=6$,$\sqrt{4×9}=\sqrt{36}=6$;
(2)$\sqrt{16}×\sqrt{25}=4×5=20$,$\sqrt{16×25}=\sqrt{400}=20$;
(3)$\sqrt{0.01}×\sqrt{0.04}=0.1×0.2=0.02$,$\sqrt{0.01×0.04}=\sqrt{0.0004}=0.02$;
(4)$\sqrt{\frac{1}{4}}×\sqrt{\frac{16}{9}}=\frac{1}{2}×\frac{4}{3}=\frac{2}{3}$,$,\sqrt{\frac{1}{4}×\frac{16}{9}}=\sqrt{\frac{4}{9}}=\frac{2}{3}$;
由上面可得,$\sqrt{a}×\sqrt{b}=\sqrt{ab}$(a≥0,b≥0).
点评 本题考查二次根式的乘除法,解题的关键是明确二次根式乘除法的计算方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.下列说法正确的个数是( )
①-4没有立方根;②-5的立方根是-$\root{3}{-5}$;③1的立方根是±1;④$\frac{1}{36}$的立方根是$\frac{1}{6}$;⑤64的立方根是4.
①-4没有立方根;②-5的立方根是-$\root{3}{-5}$;③1的立方根是±1;④$\frac{1}{36}$的立方根是$\frac{1}{6}$;⑤64的立方根是4.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
5. 如图,在方格纸上,△ABC经过变换得到△DEF,下列对变换过程的叙述正确的是( )
如图,在方格纸上,△ABC经过变换得到△DEF,下列对变换过程的叙述正确的是( )
 如图,在方格纸上,△ABC经过变换得到△DEF,下列对变换过程的叙述正确的是( )
如图,在方格纸上,△ABC经过变换得到△DEF,下列对变换过程的叙述正确的是( )| A. | △ABC绕着点A顺时针旋转90°,再向右平移7格 | |
| B. | △ABC向右平移4格,再向上平移7格 | |
| C. | △ABC绕着点A逆时针旋转90°,再向右平移7格 | |
| D. | △ABC向右平移4格,再绕着点B逆时针旋转90° |
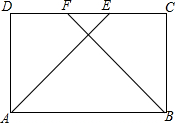 四边形ABCD中,AB∥CD,AB=CD,AE为∠A的平分线,BF为∠B的平分线,E、F在CD上,AE=BF,证明:四边形ABCD是矩形.
四边形ABCD中,AB∥CD,AB=CD,AE为∠A的平分线,BF为∠B的平分线,E、F在CD上,AE=BF,证明:四边形ABCD是矩形.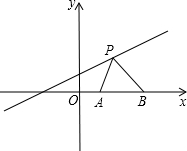 已知如图,点A(1,0),点B(2,0),点P是直线y=$\frac{1}{2}$x+1上的一个动点,PA2+PB2的最小值=$\frac{27}{5}$.
已知如图,点A(1,0),点B(2,0),点P是直线y=$\frac{1}{2}$x+1上的一个动点,PA2+PB2的最小值=$\frac{27}{5}$.
 如图,直线AB,CD相交于点O,OE⊥AB,垂足为O,∠BOD=20°,求∠COE的度数.
如图,直线AB,CD相交于点O,OE⊥AB,垂足为O,∠BOD=20°,求∠COE的度数.