题目内容
为推进郴州市创建国家森林城市工作,尽快实现“让森林走进城市,让城市拥抱森林”的构想,今年三月份,某县园林办购买了甲、乙两种树苗共1000棵,其中甲种树苗每棵40元,乙种树苗每棵50元,据相关资料表明:甲、乙两种树苗的成活率分别为85%和90%.
(1)若购买甲、乙两种树苗共用去了46500元,则购买甲、乙两种树苗各多少棵?
(2)若要使这批树苗的成活率不低于88%,则至多可购买甲种树苗多少棵?
(1)若购买甲、乙两种树苗共用去了46500元,则购买甲、乙两种树苗各多少棵?
(2)若要使这批树苗的成活率不低于88%,则至多可购买甲种树苗多少棵?
考点:二元一次方程组的应用,一元一次不等式的应用
专题:应用题
分析:(1)设购买甲、乙两种树苗各x棵和y棵,根据甲、乙两种树苗共1000颗和甲、乙两种树苗共用去了46500元,列出方程组,进行求解即可;
(2)设至多可购买甲种树苗x棵,则购买乙种树苗为(1000-x)棵,根据这批树苗的成活率不低于88%,列出不等式,求解即可.
(2)设至多可购买甲种树苗x棵,则购买乙种树苗为(1000-x)棵,根据这批树苗的成活率不低于88%,列出不等式,求解即可.
解答:解:(1)设购买甲、乙两种树苗各x棵和y棵,根据题意得:
,
解得:
,
答:购买甲、乙两种树苗各350棵和650棵;
(2)设至多可购买甲种树苗x棵,则购买乙种树苗为(1000-x)棵,根据题意得,
≥88%,
解得x≤400,
答:至多可购买甲种树苗400棵.
|
解得:
|
答:购买甲、乙两种树苗各350棵和650棵;
(2)设至多可购买甲种树苗x棵,则购买乙种树苗为(1000-x)棵,根据题意得,
| 85%x+90%(1000-x) |
| 1000 |
解得x≤400,
答:至多可购买甲种树苗400棵.
点评:此题主要考查了二元一次方程组的应用和不等式的应用,解题关键是弄清题意,找到合适的数量关系,列出方程组和不等式.

练习册系列答案
相关题目
 学校举行“文明环保,从我做起”征文比赛.现有甲、乙两班各上交30篇作文,现将两班的各30篇作文的成绩(单位:分)统计如下:
学校举行“文明环保,从我做起”征文比赛.现有甲、乙两班各上交30篇作文,现将两班的各30篇作文的成绩(单位:分)统计如下: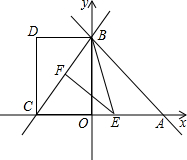 如图,在平面直角坐标系xoy中,直线
如图,在平面直角坐标系xoy中,直线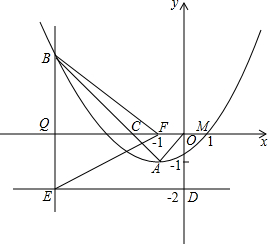 如图,抛物线y=ax2+bx+c(a≠0)的顶点为A(-1,-1),与x轴交点M(1,0).C为x轴上一点,且∠CAO=90°,线段AC的延长线交抛物线于B点,另有点F(-1,0).
如图,抛物线y=ax2+bx+c(a≠0)的顶点为A(-1,-1),与x轴交点M(1,0).C为x轴上一点,且∠CAO=90°,线段AC的延长线交抛物线于B点,另有点F(-1,0).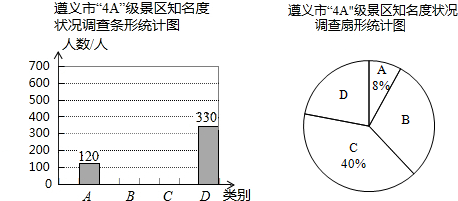
 小明听说“武黄城际列车”已经开通,便设计了如下问题:如图,以往从黄石A坐客车到武昌客运站B,现在可以在A坐城际列车到武汉青山站C,再从青山站C坐市内公共汽车到武昌客运站B.设AB=80km,BC=20km,∠ABC=120°.请你帮助小明解决以下问题:
小明听说“武黄城际列车”已经开通,便设计了如下问题:如图,以往从黄石A坐客车到武昌客运站B,现在可以在A坐城际列车到武汉青山站C,再从青山站C坐市内公共汽车到武昌客运站B.设AB=80km,BC=20km,∠ABC=120°.请你帮助小明解决以下问题: 如图,已知在平行四边形ABCD中,点E在边AB上,且AB=3EB.设
如图,已知在平行四边形ABCD中,点E在边AB上,且AB=3EB.设