��Ŀ����
 ��ͼ����ƽ��ֱ������ϵxoy�У�ֱ��y=-
��ͼ����ƽ��ֱ������ϵxoy�У�ֱ��y=-| 1 |
| 3 |
��1����m��ֵ��ֱ��BC�ı���ʽ��
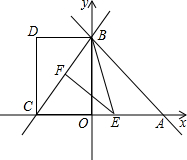
��2������D �ڸ��������ϣ����ı���OBDCΪ���Σ���������ߵı���ʽ��
��3����E��F�ֱ����߶�AC��BC�ϵĶ��㣨��E�����A��C�غϣ�������BEF=��BAO���ҡ�BEF�ǵ���������ʱ�����E�����꣮
���㣺���κ����ۺ���
ר�⣺
��������1���������ֱ����y��Ľ���B�����꣬Ȼ�����4OA=3OB����߶�OA�ij����Ӷ���õ�A�����꣬������ֱ֪�������m��ֵ��Ȼ����ݷ��۵����ʵõ���C�����꣬���ô���ϵ����ȷ��ֱ��BC�Ľ���ʽ���ɣ�
��2�������ı���OCDBΪ���κ͵�B��C������ȷ����D�����꣬������֪�ĵ�A�͵�B���������ô���ϵ����ȷ�������ߵĽ���ʽ���ɣ�
��3������֤�á�BEF�ס�BCE�����ݡ�BEFΪ���������Σ��õ���BCEΪ���������Σ�Ȼ��ֵ�CE=CB=5ʱ����BE=BCʱ����EC=EBʱ���������õ�E�����꼴�ɣ�
��2�������ı���OCDBΪ���κ͵�B��C������ȷ����D�����꣬������֪�ĵ�A�͵�B���������ô���ϵ����ȷ�������ߵĽ���ʽ���ɣ�
��3������֤�á�BEF�ס�BCE�����ݡ�BEFΪ���������Σ��õ���BCEΪ���������Σ�Ȼ��ֵ�CE=CB=5ʱ����BE=BCʱ����EC=EBʱ���������õ�E�����꼴�ɣ�
����⣺��1����x=0����ֱ��y=-
mx+4��
��ã�y=4��
���B��������0��4����
��OB=4
��4OA=3OB��
��OA=3
���A��������3��0����
��ѵ㣨3��0������y=-
mx+4��
���m=4��
�ɷ��ۿ�֪����C������Ϊ��-3��0����
��ֱ��BC�Ľ���ʽΪy=kx+b��
���������ʽ���ã�
��
��ã�
������ֱ��BCΪy=
x+4��
��2�����ı���OBDCΪ���Σ�
���D��������-3��4����
��������y=ax2+bx+c����A��B���㣬
�ཫ��A��3��0����B��0��4����D��-3��4���ֱ����y=ax2+bx+c���ã�
��ã�
��
�������ߵĽ���ʽΪy=-
x2-2x+4��
��3���ɣ�1����֪BC=BA
���BCA=��BAC��
����BEF=��BAO��
���BEF=��BCO��
���BEF�ס�BCE��
�ߡ�BEFΪ���������Σ�
��BCE����������
1����CE=CB=5ʱ����OC=3����֪��OE=2��
��E��2��0����
2����BE=BCʱ����E��A�غϣ��������⣬��ȥ��
3����EC=EBʱ�����E��x��0����
��x+3��2=x2+42��
���x=
��
��E��
��0��
���ϣ������E����Ϊ��2��0����
��0����
| 1 |
| 3 |
��ã�y=4��
���B��������0��4����
��OB=4
��4OA=3OB��
��OA=3
���A��������3��0����
��ѵ㣨3��0������y=-
| 1 |
| 3 |
���m=4��
�ɷ��ۿ�֪����C������Ϊ��-3��0����
��ֱ��BC�Ľ���ʽΪy=kx+b��
���������ʽ���ã�
|
��ã�
|
������ֱ��BCΪy=
| 4 |
| 3 |
��2�����ı���OBDCΪ���Σ�
���D��������-3��4����
��������y=ax2+bx+c����A��B���㣬
�ཫ��A��3��0����B��0��4����D��-3��4���ֱ����y=ax2+bx+c���ã�
|
��ã�
|
�������ߵĽ���ʽΪy=-
| 2 |
| 9 |
��3���ɣ�1����֪BC=BA
���BCA=��BAC��
����BEF=��BAO��
���BEF=��BCO��
���BEF�ס�BCE��
�ߡ�BEFΪ���������Σ�
��BCE����������
1����CE=CB=5ʱ����OC=3����֪��OE=2��
��E��2��0����
2����BE=BCʱ����E��A�غϣ��������⣬��ȥ��
3����EC=EBʱ�����E��x��0����
��x+3��2=x2+42��
���x=
| 7 |
| 6 |
��E��
| 7 |
| 6 |
���ϣ������E����Ϊ��2��0����
| 7 |
| 6 |
���������⿼���˶��κ������ۺ�֪ʶ����Ŀ�л������˴���ϵ������֪ʶ�����������õ��ķ������۵���ѧ˼������п����ȵ㿼��֮һ���ѶȽϴ�

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
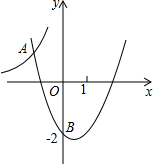 ��ͼ�����κ���y=x2+bx+c��ͼ�����B��0��-2�������뷴��������y=-
��ͼ�����κ���y=x2+bx+c��ͼ�����B��0��-2�������뷴��������y=-| 8 |
| x |
| A��y=x2-x-2 |
| B��y=x2-x+2 |
| C��y=x2+x-2 |
| D��y=x2+x+2 |
 ��֪����ͼ��ʾ��AB=AC��BD=CD��DE��AB�ڵ�E��DF��AC�ڵ�F����֤��DE=DF��
��֪����ͼ��ʾ��AB=AC��BD=CD��DE��AB�ڵ�E��DF��AC�ڵ�F����֤��DE=DF�� ��ͼ����ƽ��ֱ������ϵ�У��߳����ȵ��������������У�ÿ�������ζ���һ���������ں���y=x��ͼ���ϣ��������ҵ�3���������е�һ������A������Ϊ��8��4������Ӱ�����β��ֵ���������������μ�ΪS1��S2��S3������Sn����Sn��ֵΪ
��ͼ����ƽ��ֱ������ϵ�У��߳����ȵ��������������У�ÿ�������ζ���һ���������ں���y=x��ͼ���ϣ��������ҵ�3���������е�һ������A������Ϊ��8��4������Ӱ�����β��ֵ���������������μ�ΪS1��S2��S3������Sn����Sn��ֵΪ