题目内容
1.已知x1是关于x的一元二次方程ax2+bx+c=0(a≠0)的一个根,记△=b2-4ac,M=(2ax1+b)2,则关于△与M大小关系的下列说法中,正确的是( )| A. | △>M | B. | △=M | ||
| C. | △<M | D. | 无法确定△与M的大小 |
分析 根据题意可以先对M化简,从而可以得到M和△的关系,本题得以解决.
解答 解:∵x1是关于x的一元二次方程ax2+bx+c=0(a≠0)的一个根,
∴ax12+bx1+c=0,
∴ax12+bx1=-c,
∴M=(2ax1+b)2=$4{a}^{2}{{x}_{1}}^{2}+4ab{x}_{1}+{b}^{2}$=4a(ax12+bx1)+b2=4a÷(-c)+b2=b2-4ac=△,
故选B.
点评 本题考查根的判别式,解题的关键是明确根的判别式的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.反比例函数y=$\frac{6}{x}$图象上有三个点(-2,y1),(-1,y2),(1,y3),则y1,y2,y3的大小关系是( )
| A. | y1<y2<y3 | B. | y3<y1<y2 | C. | y2<y1<y3 | D. | y3<y2<y1 |
11.观察下列各式数:-2x,4x2,-8x3,16x4,-32x5,…则第n个式子是( )
| A. | -2n-1xn | B. | (-2)n-1xn | C. | -2nxn | D. | (-2)nxn |
 已知:两条定直线a,b在直线a上有一个定点A,在直线a上求一点B,在直线b上求一点P,使两点A、B与点P的连线总长最短.
已知:两条定直线a,b在直线a上有一个定点A,在直线a上求一点B,在直线b上求一点P,使两点A、B与点P的连线总长最短. 如图,在矩形ABCD中,AB=4,BC=2,O为AC的中点,⊙C的半径为1,过点O作⊙C的切线,E为切点,作OF⊥OE,交CD于点F,求tan∠OFC的值.
如图,在矩形ABCD中,AB=4,BC=2,O为AC的中点,⊙C的半径为1,过点O作⊙C的切线,E为切点,作OF⊥OE,交CD于点F,求tan∠OFC的值. 如图,一位牧童每天都要从A地出发赶着牛到河边饮水,然后再到B地放牧,应该怎样选择饮水的地点,才能使牛所走的路线最短?
如图,一位牧童每天都要从A地出发赶着牛到河边饮水,然后再到B地放牧,应该怎样选择饮水的地点,才能使牛所走的路线最短?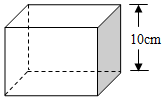 如图,某玩具厂要制作一批体积为1000cm3的长方体包装盒,其高为10cm.按设计需要,底面应做成正方形.求底面边长应是多少?
如图,某玩具厂要制作一批体积为1000cm3的长方体包装盒,其高为10cm.按设计需要,底面应做成正方形.求底面边长应是多少?

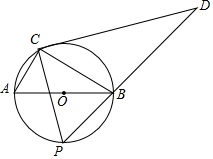 如图,⊙O的直径为4,C为⊙O上一个定点,∠ABC=30°,动点P从A点出发沿半圆弧$\widehat{AB}$向B点运动(点P与点C在直径AB的异侧),当P点到达B点时运动停止,在运动过程中,过点C作CP的垂线CD交PB的延长线于D点.
如图,⊙O的直径为4,C为⊙O上一个定点,∠ABC=30°,动点P从A点出发沿半圆弧$\widehat{AB}$向B点运动(点P与点C在直径AB的异侧),当P点到达B点时运动停止,在运动过程中,过点C作CP的垂线CD交PB的延长线于D点.