题目内容
13.使式子$\frac{x+3}{x-3}$÷$\frac{x+5}{x-4}$有意义的x值是( )| A. | x≠3,且x≠-5 | B. | x≠3,且x≠4 | ||
| C. | x≠±3 | D. | x≠3,且x≠4,且x≠-5 |
分析 分式有意义,分母不等于零,即x-3≠0,x-4≠0且$\frac{x+5}{x-4}$≠0,据此求得x的取值.
解答 解:依题意得:x-3≠0,x-4≠0且$\frac{x+5}{x-4}$≠0,
即:x-3≠0,x-4≠0且x+5≠0,
解得x≠3,且x≠4,且x≠-5.
故选:D.
点评 本题考查了分式有意义的条件.从以下三个方面透彻理解分式的概念:
(1)分式无意义?分母为零;
(2)分式有意义?分母不为零;
(3)分式值为零?分子为零且分母不为零.

练习册系列答案
相关题目
4.(x2-x-2)6=a12x12+a11x11+a10x10+…+a1x+a0,则a12+a10+a8+a6+a4+a2=( )
| A. | 64 | B. | 32 | C. | -32 | D. | -64 |
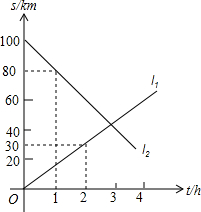 如图,l1、l2分别是甲、乙二人运动的路程与时间关系图.根据图中信息,完成下列问题:
如图,l1、l2分别是甲、乙二人运动的路程与时间关系图.根据图中信息,完成下列问题: