题目内容
18．正方形的面积x2+4xy+4y2，则它的周长为4|x+2y|．分析 根据完全平方公式，即可解答．
解答 解：∴正方形的面积x2+4xy+4y2=（x+2y）2，
∴正方形的边长为：$\sqrt{（x+2y）^{2}}$=|x+2y|，
∴正方形的周长为：4|x+2y|，
故答案为：4|x+2y|．
点评 本题考查了完全平方公式，解决本题的关键是熟记完全平方公式．
练习册系列答案
相关题目
8．
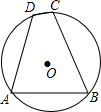如图，四边形ABCD是⊙O的内接四边形，∠BAD=80°，$\widehat{ABC}$的长为12π，$\widehat{ADC}$的长为6π，则$\widehat{BAD}$的长为（ ）
如图，四边形ABCD是⊙O的内接四边形，∠BAD=80°，$\widehat{ABC}$的长为12π，$\widehat{ADC}$的长为6π，则$\widehat{BAD}$的长为（ ）| A． | 10π | B． | 8π | C． | 5π | D． | 4π |
13．使式子$\frac{x+3}{x-3}$÷$\frac{x+5}{x-4}$有意义的x值是（ ）
| A． | x≠3，且x≠-5 | B． | x≠3，且x≠4 | ||
| C． | x≠±3 | D． | x≠3，且x≠4，且x≠-5 |
7．如果ab＜0，且ac=0，那么直线ax+by+c=0一定通过（ ）
| A． | 第一、三象限 | B． | 第二、四象限 | C． | 第一、二、三象限 | D． | 第一、三、四象限 |
8．长方形的周长是36厘米．长是宽的2倍．设长为x厘米，则下列方程正确的是（ ）
| A． | x+2x=36 | B． | x+$\frac{1}{2}$x=36 | C． | 2（x+2x）=36 | D． | 2（x+$\frac{1}{2}$x）=36 |