题目内容
16．-3-33÷$\frac{1}{3}$×3的结果是-246．分析 首先计算乘方，然后计算除法和乘法，最后计算减法，求出算式-3-33÷$\frac{1}{3}$×3的结果是多少即可．
解答 解：-3-33÷$\frac{1}{3}$×3
=-3-27÷$\frac{1}{3}$×3
=-3-243
=-246
故答案为：-246．
点评 此题主要考查了有理数的混合运算，要熟练掌握，注意明确有理数混合运算顺序：先算乘方，再算乘除，最后算加减；同级运算，应按从左到右的顺序进行计算；如果有括号，要先做括号内的运算．
练习册系列答案
相关题目
7．已知关于x方程x2-4x+m=0，如果从1、2、3、4、5、6中任选一个数作为方程常数项m，那么所得方程有实数根的概率是（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{2}{3}$ | C． | $\frac{1}{3}$ | D． | $\frac{1}{6}$ |
已知：如图，BE⊥DE，∠1=∠B，∠2=∠D，试确定AB与CD的位置关系，并说明理由．
8．
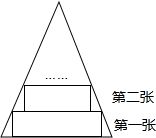如图，一张等腰三角形纸片，底边长12 cm，底边上的高位12 cm，现沿底边依次向下往上裁剪宽度均为2 cm的矩形纸条，己知剪得的纸条中有一张是正方形，则这张正方形纸条是（ ）
如图，一张等腰三角形纸片，底边长12 cm，底边上的高位12 cm，现沿底边依次向下往上裁剪宽度均为2 cm的矩形纸条，己知剪得的纸条中有一张是正方形，则这张正方形纸条是（ ）| A． | 第4张 | B． | 第5张 | C． | 第6张 | D． | .第7张 |
5．已知y=3$\sqrt{x-2}+\sqrt{2-x}$+6，则x+y的立方根是（ ）
| A． | 2 | B． | -2 | C． | ±2 | D． | 8 |
6．
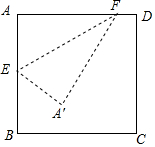如图，在边长为1的正方形ABCD中，E、F分别为线段AB、AD、上的动点，若以EF为折线翻折，A点落在正方形ABCD所在的A′点的位置，那么A'所有可能位置形成的区域面积为（ ）
如图，在边长为1的正方形ABCD中，E、F分别为线段AB、AD、上的动点，若以EF为折线翻折，A点落在正方形ABCD所在的A′点的位置，那么A'所有可能位置形成的区域面积为（ ）| A． | $\frac{1}{2}$ | B． | $\frac{π}{4}$ | C． | $\sqrt{2}$-1 | D． | $\frac{π}{2}$-1 |