题目内容
11.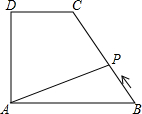 如图,在直角梯形ABCD中,∠DAB=90°,DC∥AB,动点P从点B开始沿BC-CD-DA做匀速运动,到点A终止.设点P的运动时间为t,△ABP的面积为S,则S与t的函数图象大致是( )
如图,在直角梯形ABCD中,∠DAB=90°,DC∥AB,动点P从点B开始沿BC-CD-DA做匀速运动,到点A终止.设点P的运动时间为t,△ABP的面积为S,则S与t的函数图象大致是( )| A. | 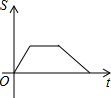 | B. | 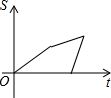 | C. | 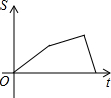 | D. | 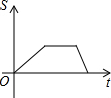 |
分析 过P作PE⊥AB于E,分三种情况:①当P在BC上时,由△ABP的面积S=$\frac{1}{2}$AB•PE,AB不变,S时t的正比例函数;
②当P在CD上时,AB、PE不变,S随t的变化不发生变化;
③当P在DA上时,S是t的一次函数,S随t的增大而减小,比P在BC上变化(减小)快;即可得出结论.
解答 解:过P作PE⊥AB于E,如图所示: 分三种情况:
分三种情况:
①当P在BC上时,
∵△ABP的面积S=$\frac{1}{2}$AB•PE,
∴S随t的增大而增大,AB不变,S时t的正比例函数;
②当P在CD上时,PE不变,S随t的增大不发生变化;
③当P在DA上时,AB不变,PE减小,S是t的一次函数,S随t的增大而减小,比P在BC上变化(减小)快;
综上所述:图象应为D.
故选:D.
点评 本题考查了动点问题的函数图象以及三角形面积的计算;根据三角形面积的计算得出面积的变化情况是解决问题的关键.

练习册系列答案
 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
3. 甲、乙两人沿同一公路从A地出发到B地,甲乘汽车,乙骑摩托车,从A地到B地的路程为120千米.若图中CD,OE分别表示甲、乙离开A地的路程S(千米)和时间t(小时)的函数关系的图象,则下列结论中错误的是( )
甲、乙两人沿同一公路从A地出发到B地,甲乘汽车,乙骑摩托车,从A地到B地的路程为120千米.若图中CD,OE分别表示甲、乙离开A地的路程S(千米)和时间t(小时)的函数关系的图象,则下列结论中错误的是( )
 甲、乙两人沿同一公路从A地出发到B地,甲乘汽车,乙骑摩托车,从A地到B地的路程为120千米.若图中CD,OE分别表示甲、乙离开A地的路程S(千米)和时间t(小时)的函数关系的图象,则下列结论中错误的是( )
甲、乙两人沿同一公路从A地出发到B地,甲乘汽车,乙骑摩托车,从A地到B地的路程为120千米.若图中CD,OE分别表示甲、乙离开A地的路程S(千米)和时间t(小时)的函数关系的图象,则下列结论中错误的是( )| A. | 甲的速度为60千米/小时 | B. | 乙从A地到B地用了3小时 | ||
| C. | 甲比乙晚出发0.5小时 | D. | 甲到达B地时,乙离A地80千米 |
20.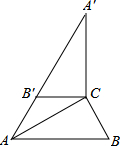 如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2.将△ABC绕点C顺时针旋转得到△A′B′C,连结AB′.若A、B′、A′在同一条直线上,则AA′的长为( )
如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2.将△ABC绕点C顺时针旋转得到△A′B′C,连结AB′.若A、B′、A′在同一条直线上,则AA′的长为( )
 如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2.将△ABC绕点C顺时针旋转得到△A′B′C,连结AB′.若A、B′、A′在同一条直线上,则AA′的长为( )
如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2.将△ABC绕点C顺时针旋转得到△A′B′C,连结AB′.若A、B′、A′在同一条直线上,则AA′的长为( )| A. | 6 | B. | $4\sqrt{3}$ | C. | $3\sqrt{3}$ | D. | 3 |
1.已知$\sqrt{a}$是二次根式,则a的值可以是( )
| A. | -2 | B. | -1 | C. | 2 | D. | -7 |
 汽车油箱中原有汽油若干,如果不再加油,那么油箱中的剩油量y(单位:L)与行驶路程x(单位:km)的寒素关系如图.
汽车油箱中原有汽油若干,如果不再加油,那么油箱中的剩油量y(单位:L)与行驶路程x(单位:km)的寒素关系如图. “龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结并反思后,和乌龟约定再赛一场.图中的函数图象刻画了“龟兔再次赛跑”的故事,x表示乌龟从起点出发所行的时间,y1表示乌龟所行的路程和时间的关系,y2表示兔子所行的路程和时间的关系,回答下列问题:
“龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结并反思后,和乌龟约定再赛一场.图中的函数图象刻画了“龟兔再次赛跑”的故事,x表示乌龟从起点出发所行的时间,y1表示乌龟所行的路程和时间的关系,y2表示兔子所行的路程和时间的关系,回答下列问题: