题目内容
1.计算:①$\frac{2}{3}$$\sqrt{3\frac{3}{4}}$×(-9$\sqrt{45}$)
②$\frac{1}{2}$$\sqrt{5}$-$\frac{5}{2}$$\sqrt{\frac{1}{5}}$+$\sqrt{45}$-$\frac{1}{2}$$\sqrt{405}$
③4$\sqrt{5}$+$\sqrt{45}$-$\sqrt{8}$+4$\sqrt{2}$
④2$\sqrt{12}$•(3$\sqrt{48}$-4$\sqrt{\frac{1}{8}}$-3$\sqrt{27}$)
分析 (1)根据二次根式的乘除法则运算;
(2)先把各二次根式化为最简二次根式,然后合并即可;
(3)先把各二次根式化为最简二次根式,然后合并即可;
(4)先把各二次根式化为最简二次根式,然后把括号内合并后进行二次根式的乘法运算.
解答 解:(1)原式=$\frac{2}{3}$×(-9)×$\sqrt{\frac{15}{4}×45}$
=-45$\sqrt{3}$;
(2)原式=$\frac{1}{2}$$\sqrt{5}$-$\frac{1}{2}$$\sqrt{5}$+3$\sqrt{5}$-$\frac{9}{2}$$\sqrt{5}$
=-$\frac{3}{2}$$\sqrt{5}$;
(3)原式=4$\sqrt{5}$+3$\sqrt{5}$-2$\sqrt{2}$+4$\sqrt{2}$
=7$\sqrt{5}$+2$\sqrt{2}$;
(4)原式=4$\sqrt{3}$(12$\sqrt{3}$-$\sqrt{2}$-9$\sqrt{3}$)
=4$\sqrt{3}$(3$\sqrt{3}$-$\sqrt{2}$)
=36-4$\sqrt{6}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
9.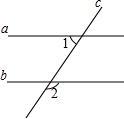 如图所示,已知a∥b,∠1=50°,则∠2等于( )
如图所示,已知a∥b,∠1=50°,则∠2等于( )
 如图所示,已知a∥b,∠1=50°,则∠2等于( )
如图所示,已知a∥b,∠1=50°,则∠2等于( )| A. | 50° | B. | 70° | C. | 110° | D. | 130° |

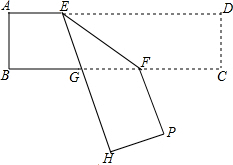 如图所示,长方形纸条ABCD沿EF折叠后,∠EFB=35°,试求∠DEH与∠BGH的大小.
如图所示,长方形纸条ABCD沿EF折叠后,∠EFB=35°,试求∠DEH与∠BGH的大小.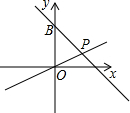 如图,一次函数y=-x+m与y轴交于点B,与正比例函数y=$\frac{1}{2}$x的图象交于点P(2,n).
如图,一次函数y=-x+m与y轴交于点B,与正比例函数y=$\frac{1}{2}$x的图象交于点P(2,n).