题目内容
12.计算:(1)($\sqrt{48}$-$\sqrt{75}$)×$\sqrt{1\frac{1}{3}}$
(2)($\sqrt{3}$-1)2-(3+$\sqrt{5}$)(3-$\sqrt{5}$)
分析 (1)先化简,再进一步合并,最后算乘法;
(2)利用完全平方公式和平方差公式计算,再进一步合并即可.
解答 解:(1)原式=(4$\sqrt{3}$-5$\sqrt{3}$)×$\frac{2}{3}$$\sqrt{3}$
=-$\sqrt{3}$×$\frac{2\sqrt{3}}{3}$
=-2;
(2)原式=4-2$\sqrt{3}$-(9-5)
=4-2$\sqrt{3}$-4
=-2$\sqrt{3}$.
点评 本题考查的是二次根式的混合运算,在进行此类运算时,一般先把二次根式化为最简二次根式的形式后再运算.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
4.已知关于x的方程(x-1)[(k-1)x+(k-3)]=0(k是常数),则下列说法中正确的是( )
| A. | 方程一定有两个不相等的实数根 | B. | 方程一定有两个实数根 | ||
| C. | 当k取某些值时,方程没有实数根 | D. | 方程一定有实数根 |
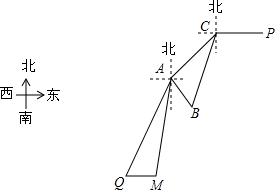 南沙群岛自古以来都是中国领土,如图,点A、B、C分别表示南沙群岛的三个小岛,岛C在岛A的北偏东45°方向,岛B在岛C的南偏西15°方向上,岛B在岛A的南偏东30°方向,且岛A、岛B两岛的距离为3海里.
南沙群岛自古以来都是中国领土,如图,点A、B、C分别表示南沙群岛的三个小岛,岛C在岛A的北偏东45°方向,岛B在岛C的南偏西15°方向上,岛B在岛A的南偏东30°方向,且岛A、岛B两岛的距离为3海里.