题目内容
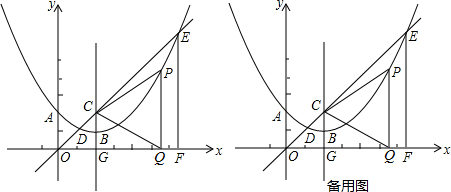
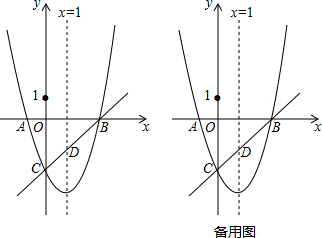
11.华盛公司有甲、乙两个销售团队,同时销售同种产品,12个月后统计得出如下信息:甲销售团队第x个月销售量y1(万件)与x之间的函数关系为y1=a(x-4)2+$\frac{1}{8}$;乙销售团队第x个月销售量y2(万件)与x之间的函数关系为y2=kx+1(1≤x≤12,x为整数).甲、乙两个销售团队在第1个月的销售量相同,均为$\frac{5}{4}$(万件)(1)分别求y1、y2的函数解析式;
(2)探求有几个月乙销售团队比甲销售团队的销量高,并求当月最多高出多少万件?
(3)直接写出共有多少个月甲、乙两个销售团队的销售量均不低于$\frac{17}{8}$万件.
分析 (1)根据甲、乙两个销售团队在第1个月的销售量相同,均为$\frac{5}{4}$(万件),代入y1、y2解方程即可;
(2)运用y2-y1=0,利用二次函数和一元二次方程以及一元二次不等式的关系解决问题;
(3)可利用不等式组解决问题.
解答 解:(1)∵甲、乙两个销售团队在第1个月的销售量相同,均为$\frac{5}{4}$(万件),
∴$\frac{5}{4}$=9a+$\frac{1}{8}$,$\frac{5}{4}$=k+1,
解得:a=$\frac{1}{8}$,k=$\frac{1}{4}$,
∴y1=$\frac{1}{8}$(x-4)2+$\frac{1}{8}$,y2=$\frac{1}{4}$x+1;
(2)y1-y2=$\frac{1}{8}$(x-4)2+$\frac{1}{8}$-$\frac{1}{4}$x+1=-$\frac{1}{8}$(x-5)2+2,
令y1-y2=0,解方程得:x1=1,x2=9,
结合函数的图象可知,当1<x<9时,y1-y2>0,即y1>y2
又x为整数,∴x=2,3,4,5,6,7,8,共有7个月乙销售团队比甲销售团队的销量高,当x=5时,当月最多高出2万件.
(3)∵甲、乙两个销售团队的销售量均不低于$\frac{17}{8}$万件.
∴$\frac{1}{8}$(x-4)2+$\frac{1}{8}$≥$\frac{17}{8}$①,$\frac{1}{4}$x+1≥$\frac{17}{8}$②,
由①得,x≤0或x≥8,由②得,x≥4.5
又∵x为整数,
∴x=8,9,10,11,12,共5个月甲、乙两个销售团队的销售量均不低于$\frac{17}{8}$万件.
点评 本题主要考查了二次函数、一次函数与方程和不等式的关系,能够熟练地运用数形结合思想,结合函数图象解不等式是解决本题的关键.

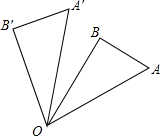 如图,在直角△OAB中,∠AOB=30°,OA=2,将△OAB绕点O逆时针旋转n°得到△OA′B′,则∠A′OB、OA′大小分别为( )
如图,在直角△OAB中,∠AOB=30°,OA=2,将△OAB绕点O逆时针旋转n°得到△OA′B′,则∠A′OB、OA′大小分别为( )| A. | n°,1 | B. | n°,2 | C. | n°-30°,1 | D. | n°-30°,2 |
| A. | 0.105×109 | B. | 1.05×109 | C. | 1.05×108 | D. | 105×106 |
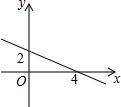 一次函数y=kx+b的图象,如图所示.
一次函数y=kx+b的图象,如图所示.