题目内容
11.已知9.972=99.4009,9.982=99.6004,9.992=99.8001,$\sqrt{997000}$之值的个位数字为8.分析 利用已知得出$\sqrt{99.7}$≈9.98,进而得出答案.
解答 解:∵9.972=99.4009,9.982=99.6004,9.992=99.8001,
∴$\sqrt{99.7}$≈9.98,
∴$\sqrt{997000}$≈998,
即其个位数字为8.
故答案为:8.
点评 此题主要考查了算术平方根,得出$\sqrt{99.7}$的近似值是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.要使分式$\frac{2}{x-2}$有意义,x必须满足的条件是( )
| A. | x≠0 | B. | x≠2 | C. | x=2 | D. | x>2 |
2.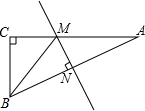 如图,在Rt△ABC中,∠C=90°,AC=12,AB=13,AB边的垂直平分线分别交AB、AC于N、M两点,则△BCM的周长为( )
如图,在Rt△ABC中,∠C=90°,AC=12,AB=13,AB边的垂直平分线分别交AB、AC于N、M两点,则△BCM的周长为( )
 如图,在Rt△ABC中,∠C=90°,AC=12,AB=13,AB边的垂直平分线分别交AB、AC于N、M两点,则△BCM的周长为( )
如图,在Rt△ABC中,∠C=90°,AC=12,AB=13,AB边的垂直平分线分别交AB、AC于N、M两点,则△BCM的周长为( )| A. | 18 | B. | 16 | C. | 17 | D. | 无法确定 |
16.一个多边形的每个内角均为108°,则这个多边形是( )边形.
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
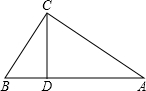 已知,如图,△ABC中,∠ACB=90°,AB=5cm,BC=3cm,CD⊥AB于D.
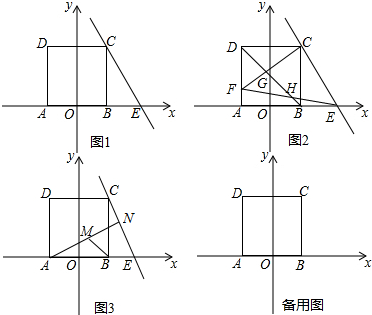
已知,如图,△ABC中,∠ACB=90°,AB=5cm,BC=3cm,CD⊥AB于D. 如图所示,图1是一个长为2m,宽为2n的长方形,沿图中的虚线剪成四个完全相同的小长方形,再按图2围成一个较大的正方形.
如图所示,图1是一个长为2m,宽为2n的长方形,沿图中的虚线剪成四个完全相同的小长方形,再按图2围成一个较大的正方形.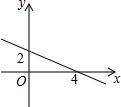 一次函数y=kx+b的图象,如图所示.
一次函数y=kx+b的图象,如图所示.