题目内容
12.(1)解方程组:$\left\{\begin{array}{l}{3x-5y=3}\\{\frac{x}{2}-\frac{y}{3}=1}\end{array}\right.$(2)解不等式组,并将解集在数轴上表示出来.
$\left\{\begin{array}{l}{\frac{x+2}{3}<1}\\{2(1-x)≤5}\end{array}\right.$.
分析 (1)方程组整理后,利用加减消元法求出解即可;
(2)分别求出不等式组中两不等式的解集,找出两解集的公共部分即可.
解答 解:(1)方程组整理得:$\left\{\begin{array}{l}{3x-5y=3①}\\{3x-2y=6②}\end{array}\right.$,
②-①得:3y=3,即y=1,
把y=1代入①得:x=$\frac{8}{3}$,
则方程组的解为$\left\{\begin{array}{l}{x=\frac{8}{3}}\\{y=1}\end{array}\right.$;
(2)$\left\{\begin{array}{l}{\frac{x+2}{3}<1①}\\{2(1-x)≤5②}\end{array}\right.$,
由①得:x<1,
由②得:x≥-$\frac{3}{2}$,
则不等式组的解集为-$\frac{3}{2}$≤x<1.
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
相关题目
2.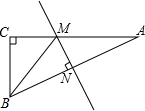 如图,在Rt△ABC中,∠C=90°,AC=12,AB=13,AB边的垂直平分线分别交AB、AC于N、M两点,则△BCM的周长为( )
如图,在Rt△ABC中,∠C=90°,AC=12,AB=13,AB边的垂直平分线分别交AB、AC于N、M两点,则△BCM的周长为( )
 如图,在Rt△ABC中,∠C=90°,AC=12,AB=13,AB边的垂直平分线分别交AB、AC于N、M两点,则△BCM的周长为( )
如图,在Rt△ABC中,∠C=90°,AC=12,AB=13,AB边的垂直平分线分别交AB、AC于N、M两点,则△BCM的周长为( )| A. | 18 | B. | 16 | C. | 17 | D. | 无法确定 |
7. 如图,已知∠1=60°,如果CD∥BE,那么∠B的度数为( )
如图,已知∠1=60°,如果CD∥BE,那么∠B的度数为( )
 如图,已知∠1=60°,如果CD∥BE,那么∠B的度数为( )
如图,已知∠1=60°,如果CD∥BE,那么∠B的度数为( )| A. | 60° | B. | 100° | C. | 110 | D. | 120° |
17.在下列长度的各组线段中,能构成直角三角形的是( )
| A. | 3,5,9 | B. | 4,6,8 | C. | 1,$\sqrt{3}$,2 | D. | $\sqrt{3}$,$\sqrt{4}$,$\sqrt{6}$ |
 如图所示,图1是一个长为2m,宽为2n的长方形,沿图中的虚线剪成四个完全相同的小长方形,再按图2围成一个较大的正方形.
如图所示,图1是一个长为2m,宽为2n的长方形,沿图中的虚线剪成四个完全相同的小长方形,再按图2围成一个较大的正方形.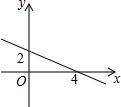 一次函数y=kx+b的图象,如图所示.
一次函数y=kx+b的图象,如图所示.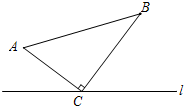 如图,△ABC中,∠ACB=90°,AC=8cm,BC=15cm,点M从A点出发沿A→C→B路径向终点运动,终点为B点,点N从B点出发沿B→C→A路径向终点运动,终点为A点,点M和N分别以每秒2m和3cm的运动速度同时开始运动,两点都要到达相应的终点时才能停止运动,分别过M和N作ME⊥l于E,NF⊥l于F.设运动时间为t秒,要使以点M,E,C为顶点的三角形与以点N,F,C为顶点的三角形全等,则t的值为$\frac{23}{5}$或7或8.
如图,△ABC中,∠ACB=90°,AC=8cm,BC=15cm,点M从A点出发沿A→C→B路径向终点运动,终点为B点,点N从B点出发沿B→C→A路径向终点运动,终点为A点,点M和N分别以每秒2m和3cm的运动速度同时开始运动,两点都要到达相应的终点时才能停止运动,分别过M和N作ME⊥l于E,NF⊥l于F.设运动时间为t秒,要使以点M,E,C为顶点的三角形与以点N,F,C为顶点的三角形全等,则t的值为$\frac{23}{5}$或7或8.