题目内容
6.在一次大学生一年级新生训练射击比赛中,某小组的成绩如表| 环数 | 6 | 7 | 8 | 9 |
| 人数 | 1 | 5 | 3 | 1 |
(2)该小组的平均成绩为多少?(要写出计算过程)
(3)若8环(含8环)以上为优秀射手,在1200名新生中有多少人可以评为优秀射手?
分析 (1)根据众数的定义即一组数据中出现次数最多的数,即可得出答案;
(2)根据平均数的计算公式进行计算即可;
(3)用1200乘以优秀选手所占的百分比即可得出答案.
解答 解:(1)∵射击7环数的人数有5个,人数最多,
∴该小组射击数据的众数是7;
故答案为:7;
(2)该小组的平均成绩为:$\frac{1}{10}$(6+7×5+8×3+9)=7.4(环);
(3)根据题意得:
1200×$\frac{4}{10}$=480(人),
答:在1200名新生中有480人可以评为优秀射手.
点评 此题考查了众数、平均数和用样本估计总体,掌握众数的定义、用样本估计总体和平均数的计算公式是本题的关键.

练习册系列答案
相关题目
13.下面有4个汽车标志图案,其中属于中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
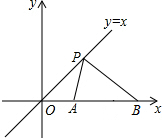 在如图所示的平面直角坐标系中,点P是直线y=x上的动点,A(2,0),B(6,0)是x轴上的两点,则PA+PB的最小值为2$\sqrt{10}$.
在如图所示的平面直角坐标系中,点P是直线y=x上的动点,A(2,0),B(6,0)是x轴上的两点,则PA+PB的最小值为2$\sqrt{10}$.