题目内容
17.已知函数y=(2m-1)x+1-3m,m为何值时:(1)这个函数的图象过原点;
(2)这个函数为一次函数;
(3)函数值y随x的增大而增大.
分析 (1)根据正比例函数的性质可得出m的值;
(2)根据一次函数的定义求出m的取值范围即可;
(3)根据一次函数的性质列出关于m的不等式,求出m的取值范围即可.
解答 解:(1)∵这个函数的图象过原点,
∴1-3m=0,解得m=$\frac{1}{3}$;
(2)∵这个函数为一次函数,
∴2m-1≠0,解得m≠$\frac{1}{2}$;
(3)∵函数值y随x的增大而增大,
∴2m-1>0,解得m>$\frac{1}{2}$.
点评 本题考查的是一次函数的图象与系数的关系,熟知一次函数的定义及增减性是解答此题的关键.

练习册系列答案
相关题目
9.下列计算正确的是( )
| A. | 2x3•3x4=5x7 | B. | 4a3•2a2=8a5 | C. | 2a3+3a3=5a6 | D. | 12x3÷4x3=3x3 |
6.在一次大学生一年级新生训练射击比赛中,某小组的成绩如表
(1)该小组射击数据的众数是7.
(2)该小组的平均成绩为多少?(要写出计算过程)
(3)若8环(含8环)以上为优秀射手,在1200名新生中有多少人可以评为优秀射手?
| 环数 | 6 | 7 | 8 | 9 |
| 人数 | 1 | 5 | 3 | 1 |
(2)该小组的平均成绩为多少?(要写出计算过程)
(3)若8环(含8环)以上为优秀射手,在1200名新生中有多少人可以评为优秀射手?
8.下列x的取值中,可以使$\sqrt{8-x}$有意义的是( )
| A. | 15 | B. | 10 | C. | 9 | D. | 0 |
5.下列计算正确的是( )
| A. | (3x)2=6x2 | B. | 3a2•2a3=6a6 | C. | (a2)6=(a4)3 | D. | (-a)3÷(-a)2=a |
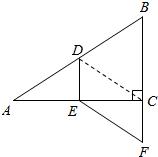 如图,在Rt△ABC中,∠ACB=90°,点D,E分别是边AB,AC的中点,延长BC至F,使CF=$\frac{1}{2}$BC,若AB=10,则EF的长是( )
如图,在Rt△ABC中,∠ACB=90°,点D,E分别是边AB,AC的中点,延长BC至F,使CF=$\frac{1}{2}$BC,若AB=10,则EF的长是( )