题目内容
14.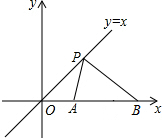 在如图所示的平面直角坐标系中,点P是直线y=x上的动点,A(2,0),B(6,0)是x轴上的两点,则PA+PB的最小值为2$\sqrt{10}$.
在如图所示的平面直角坐标系中,点P是直线y=x上的动点,A(2,0),B(6,0)是x轴上的两点,则PA+PB的最小值为2$\sqrt{10}$.
分析 作A点关于直线y=x的对称点A′,利用一次函数图象上点的坐标性质得出OA′=2,进而利用勾股定理得出结论即可.
解答  解:如图所示:作A点关于直线y=x的对称点A′,连接A′B,交直线y=x于点P,
解:如图所示:作A点关于直线y=x的对称点A′,连接A′B,交直线y=x于点P,
此时PA+PB最小,
∵OA′=2,BO=6,
∴PA+PB=A′B=$\sqrt{{2}^{2}+{6}^{2}}$=2$\sqrt{10}$.
故答案为:2$\sqrt{10}$.
点评 此题主要考查了利用轴对称求最短路线以及一次函数图象上点的特征等知识,得出P点位置是解题关键.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
9.下列计算正确的是( )
| A. | 2x3•3x4=5x7 | B. | 4a3•2a2=8a5 | C. | 2a3+3a3=5a6 | D. | 12x3÷4x3=3x3 |
19.下列标志中,是旋转对称图形但不是轴对称的有( )

| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
6.在一次大学生一年级新生训练射击比赛中,某小组的成绩如表
(1)该小组射击数据的众数是7.
(2)该小组的平均成绩为多少?(要写出计算过程)
(3)若8环(含8环)以上为优秀射手,在1200名新生中有多少人可以评为优秀射手?
| 环数 | 6 | 7 | 8 | 9 |
| 人数 | 1 | 5 | 3 | 1 |
(2)该小组的平均成绩为多少?(要写出计算过程)
(3)若8环(含8环)以上为优秀射手,在1200名新生中有多少人可以评为优秀射手?
