题目内容
17.在?ABCD中,∠DAB的平分线与BC相交,把BC分为5cm和6cm两部分,则?ABCD的周长是32或34.分析 根据AE平分∠BAD及AD∥BC可得出AB=BE,BC=BE+EC,从而根据AB、AD的长可求出平行四边形的周长.
解答 解:在平行四边形ABCD中,AD∥BC,则∠DAE=∠AEB.
∵AE平分∠BAD,
∴∠BAE=∠DAE,
∴∠BAE=∠BEA,
∴AB=BE,BC=BE+EC,
①当BE=5,EC=6时,
平行四边形ABCD的周长为:2(AB+AD)=2(5+5+6)=32.
②当BE=6,EC=5时,
平行四边形ABCD的周长为:2(AB+AD)=2(6+6+5)=34.
故答案为:32或34.
点评 本题考查平行四边形的性质,比较简单,根据题意判断出AB=BE是解答本题的关键,同学们要学会将所学知识综合起来运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.下列计算正确的是( )
| A. | 2x3•3x4=5x7 | B. | 4a3•2a2=8a5 | C. | 2a3+3a3=5a6 | D. | 12x3÷4x3=3x3 |
6.在一次大学生一年级新生训练射击比赛中,某小组的成绩如表
(1)该小组射击数据的众数是7.
(2)该小组的平均成绩为多少?(要写出计算过程)
(3)若8环(含8环)以上为优秀射手,在1200名新生中有多少人可以评为优秀射手?
| 环数 | 6 | 7 | 8 | 9 |
| 人数 | 1 | 5 | 3 | 1 |
(2)该小组的平均成绩为多少?(要写出计算过程)
(3)若8环(含8环)以上为优秀射手,在1200名新生中有多少人可以评为优秀射手?
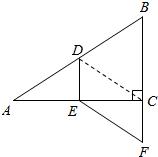 如图,在Rt△ABC中,∠ACB=90°,点D,E分别是边AB,AC的中点,延长BC至F,使CF=$\frac{1}{2}$BC,若AB=10,则EF的长是( )
如图,在Rt△ABC中,∠ACB=90°,点D,E分别是边AB,AC的中点,延长BC至F,使CF=$\frac{1}{2}$BC,若AB=10,则EF的长是( )