题目内容
11.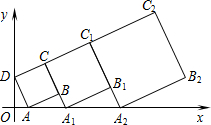 在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作第1个正方形A1B1C1C;延长C1B1交x轴于点A2,作第2个正方形A2B2C2C1,…,按这样的规律进行下去,第2016个正方形的面积是5×($\frac{3}{2}$)4030.
在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作第1个正方形A1B1C1C;延长C1B1交x轴于点A2,作第2个正方形A2B2C2C1,…,按这样的规律进行下去,第2016个正方形的面积是5×($\frac{3}{2}$)4030.
分析 先利用勾股定理求出AB=BC=AD,再用三角形相似得出A1B=$\frac{\sqrt{5}}{2}$,A2B2=($\frac{3}{2}$)2$\sqrt{5}$,找出规律A2015B2015=($\frac{3}{2}$)2015$\sqrt{5}$,即可.
解答 解:∵点A的坐标为(1,0),点D的坐标为(0,2),
∴OA=1,OD=2,BC=AB=AD=$\sqrt{5}$
∵正方形ABCD,正方形A1B1C1C,
∴∠OAD+∠A1AB=90°,∠ADO+∠OAD=90°,
∴∠A1AB=∠ADO,
∵∠AOD=∠A1BA=90°,
∴△AOD∽△A1BA,
∴$\frac{AO}{{A}_{1}B}=\frac{OD}{AB}$,
∴$\frac{1}{{A}_{1}B}=\frac{2}{\sqrt{5}}$,
∴A1B=$\frac{\sqrt{5}}{2}$,
∴A1B1=A1C=A1B+BC=$\frac{3}{2}$$\sqrt{5}$,
同理可得,A2B2=$\frac{9}{4}$$\sqrt{5}$=($\frac{3}{2}$)2$\sqrt{5}$,
同理可得,A3B3=($\frac{3}{2}$)3$\sqrt{5}$,
同理可得,A2015B2015=($\frac{3}{2}$)2015$\sqrt{5}$,
∴S第2016个正方形的面积=S正方形C2015C2015B2015A2015=[($\frac{3}{2}$)2015$\sqrt{5}$]2=5×($\frac{3}{2}$)4030,
故答案为5×($\frac{3}{2}$)4030
点评 此题是正方形的性质题,主要考查正方形的性质,勾股定理,相似三角形的性质和判定,解本题的关键是求出几个正方形的边长,找出规律.

 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案| A. | x>2 | B. | x<1 | C. | 1<x≤2 | D. | 无解 |
| A. | k>0,b>0 | B. | k>0,b<0 | C. | k<0,b>0 | D. | k<0,b<0 |
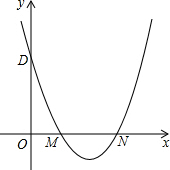 抛物线y=x2-4x+3交x轴于M,N点(M点在N点左边),交y轴于D点,点E为第一象限抛物线上的点,若∠EMN=2∠ODM,求E点坐标.
抛物线y=x2-4x+3交x轴于M,N点(M点在N点左边),交y轴于D点,点E为第一象限抛物线上的点,若∠EMN=2∠ODM,求E点坐标.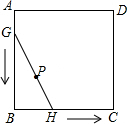 如图,正方形ABCD的边长为4,线段GH=AB,将GH的两端放在正方形的相邻的两边上同时滑动,如果G点从A点出发,沿图中所示方向按A→B→C→D→A滑动到A止,同时点H从点B出发,沿图中所示方向按B→C→D→A→B滑动到B止,在这个过程中,线段GH的中点P所经过的路线围成的图形的面积为16-4π.
如图,正方形ABCD的边长为4,线段GH=AB,将GH的两端放在正方形的相邻的两边上同时滑动,如果G点从A点出发,沿图中所示方向按A→B→C→D→A滑动到A止,同时点H从点B出发,沿图中所示方向按B→C→D→A→B滑动到B止,在这个过程中,线段GH的中点P所经过的路线围成的图形的面积为16-4π.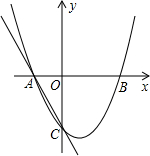 如图,抛物线y=ax2+bx+c与x轴交于A(-1,0)、B(2,0)两点,与y轴交于点C(0,-2),过A、C画直线.
如图,抛物线y=ax2+bx+c与x轴交于A(-1,0)、B(2,0)两点,与y轴交于点C(0,-2),过A、C画直线.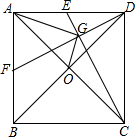 已知如图,正方形ABCD的对角线AC、BD交于O,点E、F分别是AD、AB边的中点,连接DF、CE交于点G,连接AG、OG.若AD=2,则OG=$\frac{\sqrt{10}}{5}$.
已知如图,正方形ABCD的对角线AC、BD交于O,点E、F分别是AD、AB边的中点,连接DF、CE交于点G,连接AG、OG.若AD=2,则OG=$\frac{\sqrt{10}}{5}$.