题目内容

16．不等式组$\left\{\begin{array}{l}{2x+1＞3}\\{3x-5≤1}\end{array}\right.$的解集是（　　）
A．x＞2B．x＜1C．1＜x≤2D．无解

分析 分别解出两不等式的解集再求其公共解．

解答 解：$\left\{\begin{array}{l}{2x+1＞3①}\\{3x-5≤1②}\end{array}\right.$，
由①得，x＞1，
由②得，x≤2．
故此不等式组的解集为：1＜x≤2．
故选C．

点评 本题考查的是解一元一次不等式组，熟知求不等式组解集应遵循的原则是解答此题的关键，即“同大取较大，同小去较小，小大大小中间找，大大小小解不了”．

练习册系列答案
相关题目
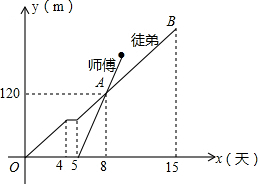6．为了检修自来水管道，由师徒两人完成，两人从管道两端开始检修，已知徒弟先修了4天后，休息了1天，接着师徒两人合做了5天，师傅被安排做其他工作，余下由徒弟单独检修完，如图是师傅和徒弟修管道的长度与工作时间的函数图象，请根据图象提供的信心解答下列问题．
（1）点A的实际意义；
（2）求直线AB的函数关系式；
（3）这个自来水管道共有多少米？
7．在平面直角坐标系中，将函数y=-2x2的图象先向右平移1个单位长度，再向上平移5个单位长度，所得图象的函数表达式是y=-2（x-1）2+5．
4．为了更好地贯彻落实国家关于“强化体育课和课外锻炼，促进青少年身心健康、体魄强健”的精神，某校大力开展体育活动．该校九年级三班同学组建了足球、篮球、乒乓球、跳绳四个体育活动小组．经调查，全班同学全员参与，各活动小组人数分布情况的扇形图和条形图如下：
（1）求该班学生人数；
（2）请你补全条形图；
（3）求跳绳人数所占扇形圆心角的度数．
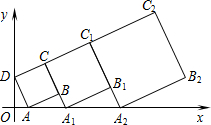11．在平面直角坐标系中，正方形ABCD的位置如图所示，点A的坐标为（1，0），点D的坐标为（0，2）．延长CB交x轴于点A1，作第1个正方形A1B1C1C；延长C1B1交x轴于点A2，作第2个正方形A2B2C2C1，…，按这样的规律进行下去，第2016个正方形的面积是5×（$\frac{3}{2}$）4030．
3．我国第一艘航空母舰“辽宁号“在海上服役，舰载机在空中飞行执行任务，需要舰上的空中加油机给补充油，如图甲所示，在空中加油过程中，设舰载机的油箱中的余油量Q1吨，加油飞机的加油油箱中的余油量为Q2吨，加油时间为t分钟Q1、Q2与t之间的函数图象如图甲所示．请回答下列问题：
（1）加油飞机的加油箱中装载了5.2吨油，将这些油全部加给舰载机需要5分钟；
（2）求加油过程中，舰载机的油箱中的余油量Q1（吨）与时间t（分钟）的函数关系式（并直接写出自变量的取值范围）；
（3）求从加油开始经过几分钟加油机的油箱中的余油量与舰载机中的余油量相同；
（4）从加完油开始（此时舰载机在空中距航空母舰700千米），航空母舰以200千米/小时向东航行，而舰载机则以800千米/小时向西飞行执行任务，舰载机距航空母舰的距离为y，飞行时间为x，则y与x之间的函数图象如图乙所示．在不能再次空中加油的情况下，为了保证舰载机安全的降落航空母舰上，一定时间必须返回．求a的最大值．
10．在Rt△ABC中，∠C=90°，BC=12，AC=9，则AB=20．
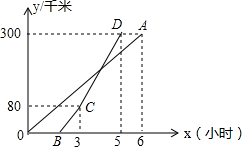7．甲乙两地相距300千米，一辆货车和一辆轿车先后从甲地出发向乙地如图、线段OA表示货车离甲地距离y（千米）与时间x（小时）之间的函数关系；折线BCD表示轿车离甲地距离y（千米）与时间x（小时）之间的函数关系，根据图象解答下列问题：
（1）轿车到达乙地后，货车距乙地多少千米？
（2）求线段CD对应的函数表达式；
（3）轿车到达乙地后，马上沿原路以CD段速度返回，求轿车从甲地出发后多长时间再与货车相遇？（结果精确到0.1）
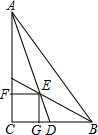8．如图，在Rt△ABC中，∠C=90°，∠BAC=40°，AD是△ABC的一条角平分线，点E，F，G分别在AD，AC，BC上，且四边形CGEF是正方形，则∠DEB的度数为（　　）
A．40°B．45°C．50°D．55°

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网