题目内容
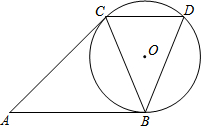 如图,AB、AC分别与⊙O相切,切点分别为B、C,过点C作CD∥AB,交⊙O于点D,连接BC、BD.
如图,AB、AC分别与⊙O相切,切点分别为B、C,过点C作CD∥AB,交⊙O于点D,连接BC、BD.(1)判断BC与BD的数量关系,并说明理由;
(2)若AB=9,BC=6,求⊙O的半径.
考点:切线的性质,相似三角形的判定与性质
专题:
分析:(1)BC=BD,连接OB,并反向延长交CD于点E.由切线的性质和已知条件易证CE=ED,所以BC=BD;
(2)连接AO,与BC交于点F,AB、AC分别与⊙O相切,切点分别为B、C,所以AO⊥BC,再证明△FAB∽△BAO,利用相似三角形的性质即可求出BO的长,即圆的半径.
(2)连接AO,与BC交于点F,AB、AC分别与⊙O相切,切点分别为B、C,所以AO⊥BC,再证明△FAB∽△BAO,利用相似三角形的性质即可求出BO的长,即圆的半径.
解答:解:(1)BC=BD.理由如下:
连接OB,并反向延长交CD于点E.
∵AB与⊙O相切,切点为B,
∴∠EBA=90°.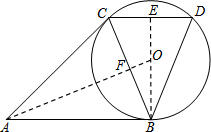
∵CD∥AB,
∴∠DEB=∠EBA=90°,即BE⊥CD.
∴CE=ED.
∴BC=BD.
(2)连接AO,与BC交于点F.
∵AB、AC分别与⊙O相切,切点分别为B、C,
∴AB=AC,∠CAO=∠BAO.
∴AO⊥BC,BF=
BC=3.
∴在Rt△AFB中,AF=
=6
.
∵∠FAB=∠BAO,∠AFB=∠ABO=90°,
∴△FAB∽△BAO.
∴
=
,即
=
.
∴BO=
,即⊙O的半径是
.
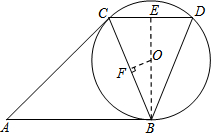
补其他方法:
∵AB、AC分别与⊙O相切,切点分别为B、C,
∴AB=AC,即△ABC是等腰三角形.
∵CD∥AB,
∴∠DCB=∠ABC.
由(1)知△BDC是等腰三角形.
∴∠ABC=∠ACB=∠BCD=∠BDC.
∴△ABC∽△BDC.
∴
=
,即
=
.
∴CD=4.
∴CE=
CD=2.
在Rt△BEC中,BE=
=4
.
作OF⊥BC,垂足为F.则BF=
BC=3.
∵∠OFB=∠CEB=90°,∠OBF=∠CBE,
∴△OBF∽△CBE.
∴
=
,即
=
.
∴OB=
,即⊙O的半径是
.
方法三:
∵AB、AC分别与⊙O相切,切点分别为B、C,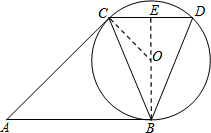
∴AB=AC,即△ABC是等腰三角形.
∵CD∥AB,
∴∠DCB=∠ABC.
由(1)知△BDC是等腰三角形.
∴∠ABC=∠ACB=∠BCD=∠BDC.
∴△ABC∽△BDC.(4分)
∴
=
,即
=
.
∴CD=4.(5分)
∴CE=
CD=2.
在Rt△BEC中,BE=
=4
.
连接OC,在Rt△CEO中,EC2+OE2=OC2.
设⊙O的半径是R,则22+(4
-R)2=R2.
解这个方程,得R=
,即⊙O的半径是
.
连接OB,并反向延长交CD于点E.
∵AB与⊙O相切,切点为B,
∴∠EBA=90°.

∵CD∥AB,
∴∠DEB=∠EBA=90°,即BE⊥CD.
∴CE=ED.
∴BC=BD.
(2)连接AO,与BC交于点F.
∵AB、AC分别与⊙O相切,切点分别为B、C,
∴AB=AC,∠CAO=∠BAO.
∴AO⊥BC,BF=
| 1 |
| 2 |
∴在Rt△AFB中,AF=
| AB2-BF2 |
| 2 |
∵∠FAB=∠BAO,∠AFB=∠ABO=90°,
∴△FAB∽△BAO.
∴
| FA |
| BA |
| FB |
| BO |
6
| ||
| 9 |
| 3 |
| BO |
∴BO=
| 9 |
| 4 |
| 2 |
| 9 |
| 4 |
| 2 |

补其他方法:
∵AB、AC分别与⊙O相切,切点分别为B、C,
∴AB=AC,即△ABC是等腰三角形.
∵CD∥AB,
∴∠DCB=∠ABC.
由(1)知△BDC是等腰三角形.
∴∠ABC=∠ACB=∠BCD=∠BDC.
∴△ABC∽△BDC.
∴
| AB |
| BC |
| BC |
| CD |
| 9 |
| 6 |
| 6 |
| CD |
∴CD=4.
∴CE=
| 1 |
| 2 |
在Rt△BEC中,BE=
| BC2-CE2 |
| 2 |
作OF⊥BC,垂足为F.则BF=
| 1 |
| 2 |
∵∠OFB=∠CEB=90°,∠OBF=∠CBE,
∴△OBF∽△CBE.
∴
| BF |
| BE |
| OB |
| CB |
| 3 | ||
4
|
| OB |
| 6 |
∴OB=
| 9 |
| 4 |
| 2 |
| 9 |
| 4 |
| 2 |
方法三:
∵AB、AC分别与⊙O相切,切点分别为B、C,

∴AB=AC,即△ABC是等腰三角形.
∵CD∥AB,
∴∠DCB=∠ABC.
由(1)知△BDC是等腰三角形.
∴∠ABC=∠ACB=∠BCD=∠BDC.
∴△ABC∽△BDC.(4分)
∴
| AB |
| BC |
| BC |
| CD |
| 9 |
| 6 |
| 6 |
| CD |
∴CD=4.(5分)
∴CE=
| 1 |
| 2 |
在Rt△BEC中,BE=
| BC2-CE2 |
| 2 |
连接OC,在Rt△CEO中,EC2+OE2=OC2.
设⊙O的半径是R,则22+(4
| 2 |
解这个方程,得R=
| 9 |
| 4 |
| 2 |
| 9 |
| 4 |
| 2 |
点评:本题考查了圆的切线性质,相似三角形的判定和性质以及勾股定理的运用的知识.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
若关于x的不等式组
在实数范围内有解,则a的取值范围为( )
|
| A、a>0 | B、a≥0 |
| C、a<0 | D、a≤0 |
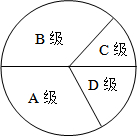 为了解我县1600名初中毕业生参加云南省数学学业水平考试的成绩情况(得分取整数),我们随机抽取了部分学生的数学成绩,将其等级情况制成不完整的统计表如下:
为了解我县1600名初中毕业生参加云南省数学学业水平考试的成绩情况(得分取整数),我们随机抽取了部分学生的数学成绩,将其等级情况制成不完整的统计表如下: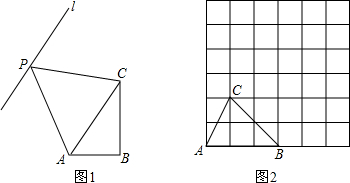
 如图,在正方形网格中,点O、A、B均在格点上,则∠AOB的正弦值是
如图,在正方形网格中,点O、A、B均在格点上,则∠AOB的正弦值是