题目内容
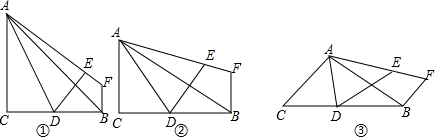
(1)操作发现:如图①,Rt△ABC中,AC=BC,∠C=90°,点D是CB的中点,将△ACD沿AD折叠后得到△AED△,过点B作BF∥AC交AE的延长线于点F,容易发现线段BF和EF的关系是 .
(2)类比思考:若将图①中“AC=BC”改成“AC≠BC”,其他条件不变,如图②,那么(1)中的发现是否仍然成立?请说明理由.
(3)拓广探究:若将图①中“Rt△ABC中,AC=BC,∠C=90°”,改为“在△ABC中”,其他条件不变,如图③,那么(1)中的发现是否仍然成立?请说明理由.
(2)类比思考:若将图①中“AC=BC”改成“AC≠BC”,其他条件不变,如图②,那么(1)中的发现是否仍然成立?请说明理由.
(3)拓广探究:若将图①中“Rt△ABC中,AC=BC,∠C=90°”,改为“在△ABC中”,其他条件不变,如图③,那么(1)中的发现是否仍然成立?请说明理由.

考点:全等三角形的判定与性质,翻折变换(折叠问题)
专题:
分析:(1)观察图形,可以发现EF=BF;
(2)如图,作辅助线;证明∠DBE=∠DEB,进而得到∠FEB=∠FBE,BF=EF.
(3)如图,作辅助线;证明∠DBE=∠DEB,进而得到∠FEB=∠FBE,BF=EF.
(2)如图,作辅助线;证明∠DBE=∠DEB,进而得到∠FEB=∠FBE,BF=EF.
(3)如图,作辅助线;证明∠DBE=∠DEB,进而得到∠FEB=∠FBE,BF=EF.
解答: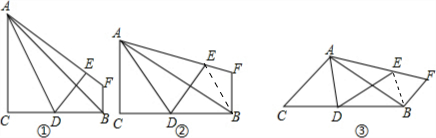 解:(1)观察图形,可以发现BF=EF.故答案为:相等.
解:(1)观察图形,可以发现BF=EF.故答案为:相等.
(2)BF=EF仍然成立;理由如下:如图②,连接BE,
由题意得:CD=DE,
∠AED=∠C;
∵BE∥AC,
∴∠FBD=∠FED=180°-∠C
∵点D是CB的中点,
∴DB=CD,DB=DE,
∴∠DBE=∠DEB,∠FEB=∠FBE,
∴BF=EF.
(3)BF=EF仍然成立;理由如下:
如图③,连接BE,
由题意得:CD=DE,
∠AED=∠C;
∵BE∥AC,
∴∠FBD=∠FED=180°-∠C
∵点D是CB的中点,
∴DB=CD,DB=DE,
∴∠DBE=∠DEB,∠FEB=∠FBE,
∴BF=EF.
 解:(1)观察图形,可以发现BF=EF.故答案为:相等.
解:(1)观察图形,可以发现BF=EF.故答案为:相等.(2)BF=EF仍然成立;理由如下:如图②,连接BE,
由题意得:CD=DE,
∠AED=∠C;
∵BE∥AC,
∴∠FBD=∠FED=180°-∠C
∵点D是CB的中点,
∴DB=CD,DB=DE,
∴∠DBE=∠DEB,∠FEB=∠FBE,
∴BF=EF.
(3)BF=EF仍然成立;理由如下:
如图③,连接BE,
由题意得:CD=DE,
∠AED=∠C;
∵BE∥AC,
∴∠FBD=∠FED=180°-∠C
∵点D是CB的中点,
∴DB=CD,DB=DE,
∴∠DBE=∠DEB,∠FEB=∠FBE,
∴BF=EF.
点评:该题主要考查了等腰三角形的判定及其性质、翻折变换的性质及其应用等几何知识点问题;解题的关键是作辅助线,构造等腰三角形,灵活运用平行线的性质等知识点来分析、解答.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
 如图,△ABC内接于⊙O,AB过点O,若∠BAC=30°,则∠B的度数为( )
如图,△ABC内接于⊙O,AB过点O,若∠BAC=30°,则∠B的度数为( )| A、55° | B、60° |
| C、65° | D、70° |
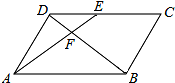 如图,在?ABCD中,E为CD上一点,连接AE、BD,且AE、BD交于点F,S△DEF:S△ABF=4:25,则DE:AB=( )
如图,在?ABCD中,E为CD上一点,连接AE、BD,且AE、BD交于点F,S△DEF:S△ABF=4:25,则DE:AB=( )| A、2:5 | B、2:3 |
| C、3:5 | D、3:2 |
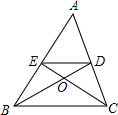 △ABC中,中线BD与CE相交于O点,S△ADE=1,则S四边形BCDE=
△ABC中,中线BD与CE相交于O点,S△ADE=1,则S四边形BCDE=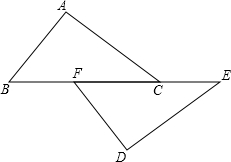 已知:如图,点B、F、C、E在一条直线上,BF=CE,AB∥DE,∠ACB=∠DFE.求证:AC=DF.
已知:如图,点B、F、C、E在一条直线上,BF=CE,AB∥DE,∠ACB=∠DFE.求证:AC=DF.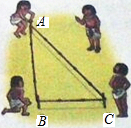 相传,古埃及人用13个等距的结把一根绳子分成等长的12段.并把它摆成△ABC的形状,如图所示,工人们按这种造型在金字塔等建筑的拐角作出直角,试问这种“张绳法”能否得到一个直角三角形呢?请同学们动手试一试,并说明理由.
相传,古埃及人用13个等距的结把一根绳子分成等长的12段.并把它摆成△ABC的形状,如图所示,工人们按这种造型在金字塔等建筑的拐角作出直角,试问这种“张绳法”能否得到一个直角三角形呢?请同学们动手试一试,并说明理由.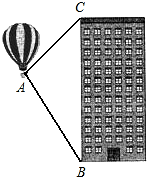 桐城市某房产公司推出热气球观房活动,热气球的探测器显示,从热气球A处看某小区内一栋高楼顶部的仰角为30°,看这栋高楼底部的俯角为60°,A处于高楼的水平距离为30m,求这栋高楼有多高?(结果精确到1m,参考数据:
桐城市某房产公司推出热气球观房活动,热气球的探测器显示,从热气球A处看某小区内一栋高楼顶部的仰角为30°,看这栋高楼底部的俯角为60°,A处于高楼的水平距离为30m,求这栋高楼有多高?(结果精确到1m,参考数据: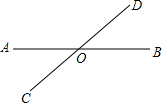 如图,直线AB、CD相交于点O,∠AOD=3∠BOD+20°.
如图,直线AB、CD相交于点O,∠AOD=3∠BOD+20°.