题目内容
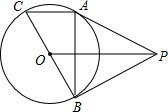 如图,P为⊙O外一点,PA、PB均为⊙O的切线,A和B是切点,BC是直径.求证:
如图,P为⊙O外一点,PA、PB均为⊙O的切线,A和B是切点,BC是直径.求证:(1)∠APB=2∠ABC;
(2)AC∥OP.
考点:切线的性质
专题:证明题
分析:(1)由切线长定理可知∠APB=2∠APO,所以只要证明∠ABC=∠APO即可;
(2)连接AB交PO于F,根据切线的性质得到PO垂直平分AB,再根据直径所对的圆周角是直角可得∠CAB=90°,于是∠CAB=∠OFB,所以AC∥OP.
(2)连接AB交PO于F,根据切线的性质得到PO垂直平分AB,再根据直径所对的圆周角是直角可得∠CAB=90°,于是∠CAB=∠OFB,所以AC∥OP.
解答:证明:(1)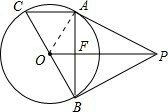 连接AO,
连接AO,
∵PA、PB均为⊙O的切线,A和B是切点,
∴∠APO=∠BPO,OA⊥AP,PA=PB,
∴∠APB=2∠APO,∠OAP=90°,PO⊥AB,
∴∠OAB+∠BAP=90°,∠BAP+∠APB=90°,
∴∠OAB=∠APB,
∵OA=OB,
∴∠OBA=∠OAB,
∴∠OBA=∠APO,
∴∠APB=2∠ABC;
(2)设AB交OP于F,
∵PA,PB是圆的切线,
∴PA=PB,
∵OA=OB
∴PO垂直平分AB.
∴∠OFB=90°.
∵BC是直径,
∴∠CAB=90°.
∴∠CAB=∠OFB.
∴AC∥OP.
 连接AO,
连接AO,∵PA、PB均为⊙O的切线,A和B是切点,
∴∠APO=∠BPO,OA⊥AP,PA=PB,
∴∠APB=2∠APO,∠OAP=90°,PO⊥AB,
∴∠OAB+∠BAP=90°,∠BAP+∠APB=90°,
∴∠OAB=∠APB,
∵OA=OB,
∴∠OBA=∠OAB,
∴∠OBA=∠APO,
∴∠APB=2∠ABC;
(2)设AB交OP于F,
∵PA,PB是圆的切线,
∴PA=PB,
∵OA=OB
∴PO垂直平分AB.
∴∠OFB=90°.
∵BC是直径,
∴∠CAB=90°.
∴∠CAB=∠OFB.
∴AC∥OP.
点评:本题考查了切线的性质、圆周角定理:在圆中,直径所对的圆周角是直角.

练习册系列答案
相关题目
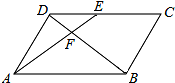 如图,在?ABCD中,E为CD上一点,连接AE、BD,且AE、BD交于点F,S△DEF:S△ABF=4:25,则DE:AB=( )
如图,在?ABCD中,E为CD上一点,连接AE、BD,且AE、BD交于点F,S△DEF:S△ABF=4:25,则DE:AB=( )| A、2:5 | B、2:3 |
| C、3:5 | D、3:2 |
 如图,已知⊙O的半径为5cm,弦AB=8cm,则圆心O到弦AB的距离是( )
如图,已知⊙O的半径为5cm,弦AB=8cm,则圆心O到弦AB的距离是( )| A、1cm | B、2cm |
| C、3cm | D、4cm |
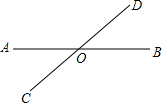 如图,直线AB、CD相交于点O,∠AOD=3∠BOD+20°.
如图,直线AB、CD相交于点O,∠AOD=3∠BOD+20°. 已知:如图,点A、B、D、E在同一直线上,AD=EB,AC=EF,AC∥EF.求证:BC=DF.
已知:如图,点A、B、D、E在同一直线上,AD=EB,AC=EF,AC∥EF.求证:BC=DF.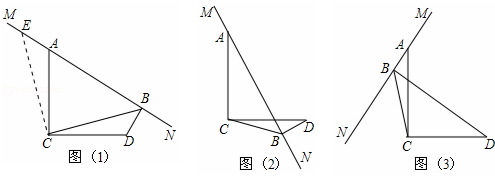
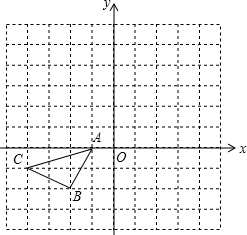 在如图所示的正方形网格中,△ABC的顶点均在格点上,请在所给直角坐标系中按要求画图和解答下列问题:
在如图所示的正方形网格中,△ABC的顶点均在格点上,请在所给直角坐标系中按要求画图和解答下列问题: 如图,求∠A+∠B+∠C+∠D+∠E+∠F的度数.
如图,求∠A+∠B+∠C+∠D+∠E+∠F的度数.