题目内容
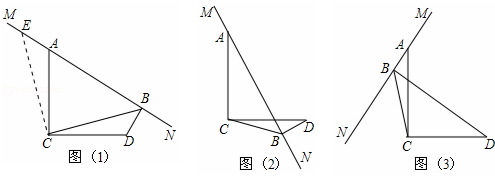
 如图,在△ABC中,∠A=55°,b=20cm,c=30cm,求S△ABC(参考数据:sin55°≈0.8192,结果精确到0.1cm2)
如图,在△ABC中,∠A=55°,b=20cm,c=30cm,求S△ABC(参考数据:sin55°≈0.8192,结果精确到0.1cm2)考点:解直角三角形
专题:计算题
分析:作CD⊥AB于D,如图在Rt△ACD中,利用∠A的正弦可得CD=20sin55°,然后根据三角形面积公式得到S△ABC=
•20sin55°•30,再进行近似计算即可.
| 1 |
| 2 |
解答:解:作CD⊥AB于D,如图,
在Rt△ACD中,∵sinA=
,
∴CD=bsinA=20sin55°,
∴S△ABC=
•CD•AB
=
•20sin55°•30
=
×20×0.8192×30
≈245.7(cm2).

在Rt△ACD中,∵sinA=
| CD |
| AC |
∴CD=bsinA=20sin55°,
∴S△ABC=
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
≈245.7(cm2).
点评:本题考查了解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
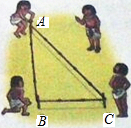 相传,古埃及人用13个等距的结把一根绳子分成等长的12段.并把它摆成△ABC的形状,如图所示,工人们按这种造型在金字塔等建筑的拐角作出直角,试问这种“张绳法”能否得到一个直角三角形呢?请同学们动手试一试,并说明理由.
相传,古埃及人用13个等距的结把一根绳子分成等长的12段.并把它摆成△ABC的形状,如图所示,工人们按这种造型在金字塔等建筑的拐角作出直角,试问这种“张绳法”能否得到一个直角三角形呢?请同学们动手试一试,并说明理由. 如图,小明和小刚的家分别在A﹑B两地,ON是去往学校的马路,他们每次上学时都约在ON上一点C,这一点与他们家的距离分别相等.请用尺规作图的方法在图中作出点C(保留作图痕迹).
如图,小明和小刚的家分别在A﹑B两地,ON是去往学校的马路,他们每次上学时都约在ON上一点C,这一点与他们家的距离分别相等.请用尺规作图的方法在图中作出点C(保留作图痕迹).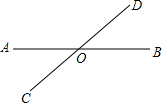 如图,直线AB、CD相交于点O,∠AOD=3∠BOD+20°.
如图,直线AB、CD相交于点O,∠AOD=3∠BOD+20°.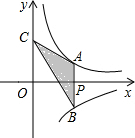 如图,过x轴正半轴上的任意一点P作y轴的平行线交反比例函数y=
如图,过x轴正半轴上的任意一点P作y轴的平行线交反比例函数y=