题目内容
15.某项工程,须在40天内完成.现有甲、乙两个工程队有意承包这项工程.经调查知道:乙工程队单独完成此项工程的时间是甲工程队单独完成此项工程时间的2倍,若甲、乙两工程队合作只需10天完成.(1)甲、乙两个工程队单独完成此项工程各需多少天?
(2)若甲工程队每天的工程费用是4.5万元,乙工程队每天的工程费用是2.5万元.请你设计一种方案,既能按时完工,又能使工程费用最少.
分析 (1)设甲工程队单独完成该工程需x天,则乙工程队单独完成该工程需2x天,根据甲、乙两工程队合作只需10天完成总任务,列方程求解;
(2)根据(1)可得,甲乙两工程队均能在规定的40天内单独完成,可分为三种方案,分别求出费用,选择费用最少的方案.
解答 解:(1)设甲工程队单独完成该工程需x天,则乙工程队单独完成该工程需2x天,
根据题意得:$\frac{10}{x}$+$\frac{10}{2x}$=1,
解得:x=15,
经检验,x=15是原方程的解,
∴当x=15时,2x=30,
答:甲工程队单独完成该工程需15天,则乙工程队单独完成该工程需30天;
(2)∵甲乙两工程队均能在规定的40天内单独完成,
∴有如下三种方案:
方案一:由甲工程队单独完成.所需费用为:4.5×15=67.5(万元);
方案二:由乙工程队单独完成.所需费用为:2.5×30=75(万元);
方案三:由甲乙两队合作完成.所需费用为:(4.5+2.5)×10=70(万元),
∵75>70>67.5,
∴应该选择甲工程队承包该项工程.
点评 本题考查了分式方程的应用,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列方程求解,注意检验.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
5.以下四个命题是真命题的是( )
| A. | 任意三点可以确定一个圆 | |
| B. | 菱形对角线相等 | |
| C. | 直角三角形斜边上的中线等于斜边的一半 | |
| D. | “打开电视机,中央一套正在直播巴西世界杯足球赛”是必然事件 |
6.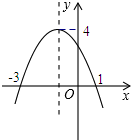 若二次函数y=ax2+bx+c(a<0)的图象如图所示,且关于x的方程ax2+bx+c=k有两个不相等的实根,则常数k的取值范围是( )
若二次函数y=ax2+bx+c(a<0)的图象如图所示,且关于x的方程ax2+bx+c=k有两个不相等的实根,则常数k的取值范围是( )
 若二次函数y=ax2+bx+c(a<0)的图象如图所示,且关于x的方程ax2+bx+c=k有两个不相等的实根,则常数k的取值范围是( )
若二次函数y=ax2+bx+c(a<0)的图象如图所示,且关于x的方程ax2+bx+c=k有两个不相等的实根,则常数k的取值范围是( )| A. | 0<k<4 | B. | -3<k<1 | C. | k<-3或k>1 | D. | k<4 |