题目内容
6.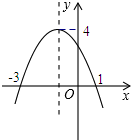 若二次函数y=ax2+bx+c(a<0)的图象如图所示,且关于x的方程ax2+bx+c=k有两个不相等的实根,则常数k的取值范围是( )
若二次函数y=ax2+bx+c(a<0)的图象如图所示,且关于x的方程ax2+bx+c=k有两个不相等的实根,则常数k的取值范围是( )| A. | 0<k<4 | B. | -3<k<1 | C. | k<-3或k>1 | D. | k<4 |
分析 根据图象信息确定抛物线的对称轴、与x轴的交点,利用待定系数法求出抛物线的解析式,得到关于x的一元二次方程,根据方程有两个不相等的实根时,判别式大于0,求出k的取值范围.
解答 解:由图象可知,抛物线的对称轴为x=-1,
∴顶点坐标为(-1,4),
设抛物线的解析式为:y=a(x+1)2+4,
把(1,0)代入解析式得,a=-1,
∴解析式为:y=-x2-2x+3,
方程=-x2-2x+3=k有两个不相等的实根,
△=4+12-4k>0,
解得:k<4.
故选:D.
点评 本题考查的是待定系数法求二次函数的解析式和一元二次方程的根的判别式的运用,正确获取图象信息是解题的关键,运用待定系数法时,选择合适的解析式的形式有助于求出解析式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.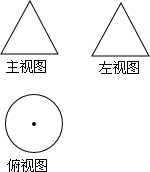 一个几何体的三视图如图所示,其中主视图与左视图都是边长为2的等边三角形,则这个几何体的侧面积为( )
一个几何体的三视图如图所示,其中主视图与左视图都是边长为2的等边三角形,则这个几何体的侧面积为( )
 一个几何体的三视图如图所示,其中主视图与左视图都是边长为2的等边三角形,则这个几何体的侧面积为( )
一个几何体的三视图如图所示,其中主视图与左视图都是边长为2的等边三角形,则这个几何体的侧面积为( )| A. | 4π | B. | 3π | C. | 2π | D. | $\sqrt{3}$π |