题目内容
20.若方程组$\left\{\begin{array}{l}{x+y=3}\\{kx-2y=9}\end{array}\right.$中x<0,则k的取值范围是k<-2.分析 根据题意将原式变形,进而得出x=$\frac{15}{2+k}$<0,求出即可.
解答 解:$\left\{\begin{array}{l}{x+y=3①}\\{kx-2y=9②}\end{array}\right.$
①×2+②得:
(2+k)x=15,
则x=$\frac{15}{2+k}$<0,
则2+k<0,
解得:k<-2.
故答案为:k<-2.
点评 此题主要考查了二元一次方程组的解,得出x的值是解题关键.

练习册系列答案
相关题目
10.计算a3•(-$\frac{1}{a}$)2的结果是( )
| A. | a | B. | a5 | C. | a6 | D. | a4 |
5.在平面直角坐标系中,若点P(m,1)在第二象限,则点Q(-m,0)在( )
| A. | x轴正半轴上 | B. | y轴正半轴上 | C. | x轴负半轴上 | D. | y轴负半轴上 |
9.下列各组数据中,能构成三角形的是( )
| A. | 2cm,2cm,4cm | B. | 3cm,3cm,4cm | C. | 4cm,9cm,3cm | D. | 2cm,1cm,5cm |
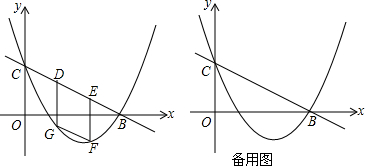
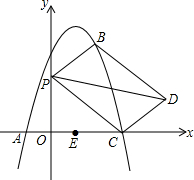 如图,抛物线y=ax2+bx+c经过点A(-1,0),E(0,5),B(2,5)三点,抛物线与x轴的另一个交点为C点,点P为y轴上一动点,作平行四边形BPCD.
如图,抛物线y=ax2+bx+c经过点A(-1,0),E(0,5),B(2,5)三点,抛物线与x轴的另一个交点为C点,点P为y轴上一动点,作平行四边形BPCD.