题目内容
4.计算:20102-20092+20082-…+22-12=2021055.分析 分组使用平方差公式,再利用等差数列求和公式解题.
解答 解:20102-20092+20082-…+22-12
=(20102-20092)+(20082-20072)…+(22-12)
=(2010-2009)×(2010+2009)+(2008-2007)×(2008+2007)+…+(2-1)×(2+1)
=2010+2009+2008+2007+…+2+1
=(2010+1)×2010÷2
=2021055.
故答案为:2021055.
点评 本题考查了平方差公式的运用,注意分组后两数的差都为1,所有两数的和组成自然数求和.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
14.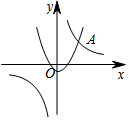 如图,抛物线y=x2+m与双曲线y=$\frac{k}{x}$的交点A的横坐标是1,则关于x的不等式$\frac{k}{x}$+x2+m<0的解集是( )
如图,抛物线y=x2+m与双曲线y=$\frac{k}{x}$的交点A的横坐标是1,则关于x的不等式$\frac{k}{x}$+x2+m<0的解集是( )
 如图,抛物线y=x2+m与双曲线y=$\frac{k}{x}$的交点A的横坐标是1,则关于x的不等式$\frac{k}{x}$+x2+m<0的解集是( )
如图,抛物线y=x2+m与双曲线y=$\frac{k}{x}$的交点A的横坐标是1,则关于x的不等式$\frac{k}{x}$+x2+m<0的解集是( )| A. | x>1 | B. | x<-1 | C. | 0<x<1 | D. | -1<x<0 |
15.一次函数y=-$\frac{4}{3}$x+1的图象与两坐标轴所围成的三角形的面积为( )
| A. | $\frac{3}{4}$ | B. | $\frac{3}{8}$ | C. | $\frac{4}{3}$ | D. | $\frac{8}{3}$ |
13.如图是某一计算程序,例如:当输入x=150时,输出结果是301;当输入x=100时,输出结果是403;若输入x的值是正整数,输出结果是407,则满足条件的x的值最多有( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
14.已知x>2,则下列变形正确的是( )
| A. | -x<2 | B. | 若y>2,则x-y>0 | C. | -$\frac{1}{2}$x+2<1 | D. | 若y>2,则$\frac{x}{y}>1$ |
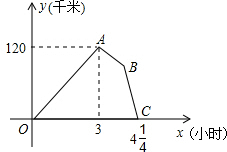 快车和慢车同时从甲地出发,以各自的速度匀速向乙地行驶,快车到达乙地后停留了45分钟,立即按原路以另一速度匀速返回,直至与慢车相遇.已知慢车的速度为60千米/时,两车之间的距离y(千米)与两车行驶时间x(小时)之间的函数图象如图所示,则快车从乙地返回时的速度为90千米/时.
快车和慢车同时从甲地出发,以各自的速度匀速向乙地行驶,快车到达乙地后停留了45分钟,立即按原路以另一速度匀速返回,直至与慢车相遇.已知慢车的速度为60千米/时,两车之间的距离y(千米)与两车行驶时间x(小时)之间的函数图象如图所示,则快车从乙地返回时的速度为90千米/时.