题目内容
10.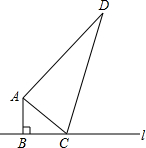 如图,∠ABC=90°,AB=6cm,AD=24cm,BC+CD=34cm,C是直线l上一动点,请你探索当C离B多远时,△ACD是一个以CD为斜边的直角三角形?
如图,∠ABC=90°,AB=6cm,AD=24cm,BC+CD=34cm,C是直线l上一动点,请你探索当C离B多远时,△ACD是一个以CD为斜边的直角三角形?
分析 设BC=xcm,则CD=(34-x)cm,再根据勾股定理及勾股定理的逆定理列出方程,求出x的值即可.
解答 解:设BC=xcm时,三角形ACD是以DC为斜边的直角三角形,
∵BC+CD=34,
∴CD=34-x,
在Rt△ABC中,AC2=AB2+BC2=36+x2,
在Rt△ACD中,AC2=CD2-AD2=(34-x)2-576,
∴36+x2=(34-x)2-576,
解得x=8.
∴当C离点B8cm时,△ACD是以DC为斜边的直角三角形.
点评 本题考查的是勾股定理的逆定理,熟知如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形是解答此题的关键.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
20.已知x=-1是方程2x2+ax-5=0的一个根,则a的值是( )
| A. | -3 | B. | -4 | C. | 3 | D. | 7 |
1.在平面直角坐标系内,将直线y=-3x向下平移6个单位,得到直线所对应的解析式是( )
| A. | y=-3x+6 | B. | y=-3x-6 | C. | y=-4x | D. | y=-2x |
5.下列命题:①若三条线段的比为1:1:$\sqrt{2}$,则它们组成一个等腰直角三角形;②两条对角线相等的平行四边形是矩形;③对角线互相垂直的四边形是菱形;④两个邻角相等的平行四边形是矩形中,其中正确命题的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
15.下列多项式中,不能用公式法分解因式的是( )
| A. | (x+y)2+12(x+y)+36 | B. | -x2+2xy-y2 | C. | -4x2+9y2 | D. | x2+y2 |
2.已知甲、乙两种水稻实验品种连续5年的平均单位面积产量如下(单位:吨/公顷)
经计算,甲乙的平均数均为10,试根据这组数据估计乙种水稻品种的产量较稳定.
| 品种 | 第1年 | 第2年 | 第3年 | 第4年 | 第5年 |
| 甲 | 9.4 | 10.3 | 10.8 | 9.7 | 9.8 |
| 乙 | 9.8 | 9.9 | 10.1 | 10 | 10.2 |
19.下列二次根式中属于最简二次根式的是( )
| A. | $\sqrt{3}$ | B. | $\sqrt{8}$ | C. | $\sqrt{\frac{1}{2}}$ | D. | $\sqrt{12}$ |