题目内容
12.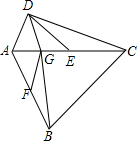 如图,四边形ABCD中,∠ADC=90°,AC=CB,E,F分别是AC,AB的中点,且∠DEA=∠ACB=45°,BG⊥AE于G,
如图,四边形ABCD中,∠ADC=90°,AC=CB,E,F分别是AC,AB的中点,且∠DEA=∠ACB=45°,BG⊥AE于G,(1)求证:四边形AFGD是菱形;
(2)若AC=BC=10,求菱形AFGD的面积.
分析 (1)先证明△EDA∽△CAB,并且DE:AC=1:2,所以AD=$\frac{1}{2}$AB=AF,易证△ADG≌△AFG,所以DG=FG,由AF=GF,可知AD=DG=FG=AF,即可证明四边形AFGD是菱形;
(2)由(1)知△ADG≌△AFG,又AF=FB,所以S△AGB=2S△AFG=S菱形AFGD,由BC=10,BG⊥AE,∠ACB=45°,知BG=GC=5$\sqrt{2}$,AG=10-5$\sqrt{2}$,S△AGB=$\frac{1}{2}$×AG×BG=25$\sqrt{2}$-25.
解答 解:(1)∵∠ADC=90°,E是AC的中点,
∴DE=AE=$\frac{1}{2}$AC,
∵AC=CB,
∴DE=AE=$\frac{1}{2}$AC=$\frac{1}{2}$BC,
∵∠DEA=∠ACB=45°,
∴△EDA∽△CAB,AD=$\frac{1}{2}$AB,
∵BG⊥AE于G,F是AB的中点,
∴AF=FG=$\frac{1}{2}$AB=AD,
在△ADG和△AFG中,
$\left\{\begin{array}{l}{AD=AF}\\{∠DAG=∠FAG}\\{AG=AG}\end{array}\right.$,
∴△ADG≌△AFG,
∴DG=FG,
∴AD=DG=FG=AF,
∴四边形AFGD是菱形;
(2)由(1)知△ADG≌△AFG,又AF=FB,
∴S△AGB=2S△AFG=S菱形AFGD,
∵BG⊥AE,∠ACB=45°,
∴△GBC是等腰直角三角形,
∵BC=10,
∴BG=GC=5$\sqrt{2}$,AG=10-5$\sqrt{2}$,
∴S△AGB=$\frac{1}{2}$×AG×BG=25$\sqrt{2}$-25,
∴S菱形AFGD=25$\sqrt{2}$-25.
点评 本题主要考查了菱形的判定、相似三角形的判定与性质、全等三角形的判定与性质、直角三角形的性质、等积变换等知识,有一定的综合性,证明△EDA∽△CAB是解决问题的关键.

 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案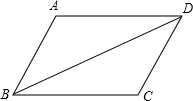 在平行四边形ABCD中,∠BAD=110°,∠ABD=30°,则∠CBD度数为( )
在平行四边形ABCD中,∠BAD=110°,∠ABD=30°,则∠CBD度数为( )| A. | 30° | B. | 40° | C. | 70° | D. | 50° |
| A. | 2m | B. | 8m | C. | 10m | D. | 12m |
| A. | -3 | B. | -4 | C. | 3 | D. | 7 |
| A. | x<y | B. | x>y | C. | x≤y | D. | x≥y |
| A. | y=-3x+6 | B. | y=-3x-6 | C. | y=-4x | D. | y=-2x |
| 品种 | 第1年 | 第2年 | 第3年 | 第4年 | 第5年 |
| 甲 | 9.4 | 10.3 | 10.8 | 9.7 | 9.8 |
| 乙 | 9.8 | 9.9 | 10.1 | 10 | 10.2 |
