题目内容
2.Rt△ABC中,∠ACB=90°,CD⊥AB于D,AD=4,BD=9,则CD=6.分析 根据两角相等证明△ACD∽△CBD,列比例式代入可得结论.
解答  解:∵∠ACB=90°,
解:∵∠ACB=90°,
∴∠ACD+∠BCD=90°,
∵CD⊥AB,
∴∠ADC=∠BDC=90°,
∴∠ACD+∠A=90°,
∴∠BCD=∠A,
∴△ACD∽△CBD,
∴$\frac{CD}{BD}=\frac{AD}{CD}$,
∵AD=4,BD=9,
∴CD2=4×9=36,
∴CD=6,
故答案为:6.
点评 本题考查了相似三角形的判定和性质、直角三角形的性质,明确同角的余角相等,为证明三角形相似打基础,这在三角形相似证明角相等时经常运用,要熟练掌握.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目
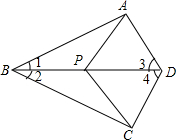 如图,已知∠1=∠2,∠3=∠4,点P是BC上任意一点,求证:PA=PC.
如图,已知∠1=∠2,∠3=∠4,点P是BC上任意一点,求证:PA=PC. 如图,BE=CD,∠1=∠2,则AB=AC吗?为什么?
如图,BE=CD,∠1=∠2,则AB=AC吗?为什么? 已知:如图,ED⊥AB,FC⊥AB,垂足分别为D、C,AE‖BF,且AE=BF.求证:AC=BD.
已知:如图,ED⊥AB,FC⊥AB,垂足分别为D、C,AE‖BF,且AE=BF.求证:AC=BD.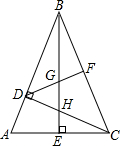 如图,在△ABC中∠ABC=45°,CD⊥BA,BE⊥AC,F为BC中点,∠ABE=∠CBE
如图,在△ABC中∠ABC=45°,CD⊥BA,BE⊥AC,F为BC中点,∠ABE=∠CBE 如图所示,A,E,F,C在一条直线上,AE=CF,过E,F分别作DE⊥AC于E,BF⊥AC于F,AC、BD交于点G,若AB=CD.
如图所示,A,E,F,C在一条直线上,AE=CF,过E,F分别作DE⊥AC于E,BF⊥AC于F,AC、BD交于点G,若AB=CD.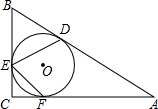 如图,在Rt△ABC中,∠C=90°,∠B=58°,内切圆O与边AB,BC,CA分别相切于点D,E,F,则∠DEF的度数为74°.
如图,在Rt△ABC中,∠C=90°,∠B=58°,内切圆O与边AB,BC,CA分别相切于点D,E,F,则∠DEF的度数为74°.