题目内容
14.我们知道,一元二次方程x2=-1没有实数根,即不存在一个实数的平方等于-1.若我们规定一个新数“i”,使其满足i2=-1(即方程x2=-1有一个根为i).并且进一步规定:一切实数可以与新数进行四则运算,且原有运算律和运算法则仍然成立,于是有i1=i,i2=-1,i3=i2•i=(-1)•i=-i,i4=(i2)2=(-1)2=1,从而对于任意正整数n,我们可以得到i4n+1=i4n•i=(i4)n•i=i,同理可得i4n+2=-1,i4n+3=-i,i4n=1.那么i+i2+i3+i4+…+i2015+i2016的值为0.分析 利用i1=i,i2=-1,i3=i2•i=(-1)•i=-i,i4=(i2)2=(-1)2=1,将原式化简整理后即可发现每四个数一周期循环,且每周期的和为0,据此可得.
解答 解:i+i2+i3+i4+…+i2015+i2016=i-1-i+1+i-1-i+1+…+1=0,
故答案为:0.
点评 本题主要考查一元二次方程的解,根据题意得出化简后每四个数一周期循环,且每周期的和为0.

练习册系列答案
相关题目
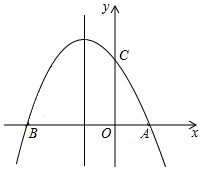 如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-1,且抛物线经过A(1,0),C(0,3)两点,与x轴相交于点B.
如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-1,且抛物线经过A(1,0),C(0,3)两点,与x轴相交于点B. 如图所示,已知点D、E、F分别是边BC,AC,DC的中点,△EFC的面积为6cm2,则△ABC的面积为48cm2.
如图所示,已知点D、E、F分别是边BC,AC,DC的中点,△EFC的面积为6cm2,则△ABC的面积为48cm2. 如图,在反比例函数y=$\frac{4}{x}$(x>0)的图象上,有点P1,P2,P3,P4…Pn(n为正整数,且n≥1).它们的横坐标依次为1,2,3,4…n(n为正整数,且n≥1),分别过这些点作x轴与y轴的垂线,连接相邻两点,图中所构成的阴影部分的面积从左到右依次为S1,S2,S3…Sn-1(n为正整数,且n≥2),那么S2+S3+S4+…S7=$\frac{3}{4}$.
如图,在反比例函数y=$\frac{4}{x}$(x>0)的图象上,有点P1,P2,P3,P4…Pn(n为正整数,且n≥1).它们的横坐标依次为1,2,3,4…n(n为正整数,且n≥1),分别过这些点作x轴与y轴的垂线,连接相邻两点,图中所构成的阴影部分的面积从左到右依次为S1,S2,S3…Sn-1(n为正整数,且n≥2),那么S2+S3+S4+…S7=$\frac{3}{4}$.