题目内容
12.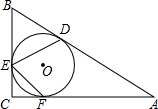 如图,在Rt△ABC中,∠C=90°,∠B=58°,内切圆O与边AB,BC,CA分别相切于点D,E,F,则∠DEF的度数为74°.
如图,在Rt△ABC中,∠C=90°,∠B=58°,内切圆O与边AB,BC,CA分别相切于点D,E,F,则∠DEF的度数为74°.
分析 连接OD、OF,根据三角形内角和定理求出∠A,根据切线的性质得到OD⊥AB,OF⊥AC,求出∠DOF,根据圆周角定理解答即可.
解答 解: 连接OD、OF,
连接OD、OF,
∵∠C=90°,∠B=58°,
∴∠A=90°-58°=32°,
∵内切圆O与边AB,CA分别相切于点D,F,
∴OD⊥AB,OF⊥AC,
∴∠DOF=180°-32°=148°,
由圆周角定理得,∠DEF=$\frac{1}{2}$∠DOF=74°,
故答案为:74°.
点评 本题考查的是三角形的内切圆和内心的概念和性质,掌握切线的性质、圆周角定理、三角形内角和定理是解题的关键.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
1. 如图,小明从路灯下A处向前走了5米,发现自己在地面上的影子长DE是2米,如果小明的身高为1.6米,那么路灯离地面的高度AB是( )
如图,小明从路灯下A处向前走了5米,发现自己在地面上的影子长DE是2米,如果小明的身高为1.6米,那么路灯离地面的高度AB是( )
 如图,小明从路灯下A处向前走了5米,发现自己在地面上的影子长DE是2米,如果小明的身高为1.6米,那么路灯离地面的高度AB是( )
如图,小明从路灯下A处向前走了5米,发现自己在地面上的影子长DE是2米,如果小明的身高为1.6米,那么路灯离地面的高度AB是( )| A. | 4米 | B. | 5.6米 | C. | 2.2米 | D. | 12.5米 |
2. 如图,△ABC的顶点都是正方形网格中的格点,则tan∠ABC等于( )
如图,△ABC的顶点都是正方形网格中的格点,则tan∠ABC等于( )
 如图,△ABC的顶点都是正方形网格中的格点,则tan∠ABC等于( )
如图,△ABC的顶点都是正方形网格中的格点,则tan∠ABC等于( )| A. | $\frac{\sqrt{5}}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | 2 |
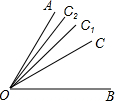 如图,∠AOB=60°,OC是∠AOB的平分线,OC1是∠AOC的平分线,OC2是∠AOC1的平分线,…,OCn是∠AOCn-1的平分线,则∠AOCn=$\frac{1}{{2}^{n+1}}$×60°.
如图,∠AOB=60°,OC是∠AOB的平分线,OC1是∠AOC的平分线,OC2是∠AOC1的平分线,…,OCn是∠AOCn-1的平分线,则∠AOCn=$\frac{1}{{2}^{n+1}}$×60°. 如图,在反比例函数y=$\frac{4}{x}$(x>0)的图象上,有点P1,P2,P3,P4…Pn(n为正整数,且n≥1).它们的横坐标依次为1,2,3,4…n(n为正整数,且n≥1),分别过这些点作x轴与y轴的垂线,连接相邻两点,图中所构成的阴影部分的面积从左到右依次为S1,S2,S3…Sn-1(n为正整数,且n≥2),那么S2+S3+S4+…S7=$\frac{3}{4}$.
如图,在反比例函数y=$\frac{4}{x}$(x>0)的图象上,有点P1,P2,P3,P4…Pn(n为正整数,且n≥1).它们的横坐标依次为1,2,3,4…n(n为正整数,且n≥1),分别过这些点作x轴与y轴的垂线,连接相邻两点,图中所构成的阴影部分的面积从左到右依次为S1,S2,S3…Sn-1(n为正整数,且n≥2),那么S2+S3+S4+…S7=$\frac{3}{4}$.