题目内容
11. 如图所示,A,E,F,C在一条直线上,AE=CF,过E,F分别作DE⊥AC于E,BF⊥AC于F,AC、BD交于点G,若AB=CD.
如图所示,A,E,F,C在一条直线上,AE=CF,过E,F分别作DE⊥AC于E,BF⊥AC于F,AC、BD交于点G,若AB=CD.(1)求证:BG=DG;
(2)若将△DEC在直线AC上移动,当点E在点F右侧时,其余条件不变,上述结论是否仍然成立?请画出示意图(不需证明).
(1)证明:
(2)结论:
示意图:
分析 (1)由条件可求得AF=CE,可利用HL证明Rt△ABF≌Rt△CDE,可得BF=DE,再证明△DEG≌△BFG即可;
(2)同(1)的方法可证明结论仍然成立.
解答 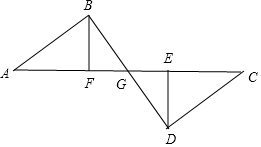 (1)证明:
(1)证明:
∵DE⊥AC于E,BF⊥AC于F,
∴∠DEC=∠BFA=90°,
∵AE=CF,
∴AE+EF=CF+EF,即AF=CE,
在Rt△ABF和Rt△CDE中
$\left\{\begin{array}{l}AB=CD\\ AF=CE\end{array}\right.$
∴Rt△ABF≌Rt△CDE(HL),
∴BF=DE
在△DEG和△BFG中
$\left\{\begin{array}{l}{∠DEG=∠BFG}\\{∠EGD=∠FGB}\\{DE=BF}\end{array}\right.$
∴△DEG≌△BFG(AAS),
∴BG=DG;
(2)结论不变.
证明方法同(1).
图形如图所示.
点评 本题主要考查全等三角形的判定和性质,掌握全等三角形的判定方法(即SSS、SAS、ASA、AAS和HL)和性质(即全等三角形的对应边、对应角相等)是解题的关键.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
1.黑板上写有$1,\frac{1}{2},\frac{1}{3},…,\frac{1}{100}$共100个数字.每次操作先从黑板上的数中选取2个数a,b,然后删去a,b,并在黑板上写上数a+b+ab,则经过99次操作后,黑板上剩下的数是( )
| A. | 2012 | B. | 101 | C. | 100 | D. | 99 |
16. 数a、b在数轴上的位置如图,则下列结论正确的是( )
数a、b在数轴上的位置如图,则下列结论正确的是( )
 数a、b在数轴上的位置如图,则下列结论正确的是( )
数a、b在数轴上的位置如图,则下列结论正确的是( )| A. | a<0 | B. | a>1 | C. | b<-1 | D. | b>-1 |
1. 如图,小明从路灯下A处向前走了5米,发现自己在地面上的影子长DE是2米,如果小明的身高为1.6米,那么路灯离地面的高度AB是( )
如图,小明从路灯下A处向前走了5米,发现自己在地面上的影子长DE是2米,如果小明的身高为1.6米,那么路灯离地面的高度AB是( )
 如图,小明从路灯下A处向前走了5米,发现自己在地面上的影子长DE是2米,如果小明的身高为1.6米,那么路灯离地面的高度AB是( )
如图,小明从路灯下A处向前走了5米,发现自己在地面上的影子长DE是2米,如果小明的身高为1.6米,那么路灯离地面的高度AB是( )| A. | 4米 | B. | 5.6米 | C. | 2.2米 | D. | 12.5米 |
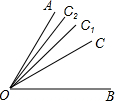 如图,∠AOB=60°,OC是∠AOB的平分线,OC1是∠AOC的平分线,OC2是∠AOC1的平分线,…,OCn是∠AOCn-1的平分线,则∠AOCn=$\frac{1}{{2}^{n+1}}$×60°.
如图,∠AOB=60°,OC是∠AOB的平分线,OC1是∠AOC的平分线,OC2是∠AOC1的平分线,…,OCn是∠AOCn-1的平分线,则∠AOCn=$\frac{1}{{2}^{n+1}}$×60°.