题目内容
10．
如图，BE=CD，∠1=∠2，则AB=AC吗？为什么？
分析 根据AAS即可证明△ABE≌△ACD，再根据全等三角形的性质即可求解．
解答 解：∵∠1=∠2，
∴∠ADC=∠AEB，
在△ABE和△ACD中，
$\left\{\begin{array}{l}{∠A=∠A}\\{∠ADC=∠AEB}\\{BE=CD}\end{array}\right.$，
∴△ABE≌△ACD（AAS）
∴AB=AC（全等三角形的对应边相等）．
点评 本题考查了全等三角形的判定与性质，在应用全等三角形的判定时，要注意三角形间的公共边和公共角，必要时添加适当辅助线构造三角形．
练习册系列答案
举一反三期末百分冲刺卷系列答案
相关题目
1．黑板上写有$1，\frac{1}{2}，\frac{1}{3}，…，\frac{1}{100}$共100个数字．每次操作先从黑板上的数中选取2个数a，b，然后删去a，b，并在黑板上写上数a+b+ab，则经过99次操作后，黑板上剩下的数是（ ）
| A． | 2012 | B． | 101 | C． | 100 | D． | 99 |
如图所示，已知点D、E、F分别是边BC，AC，DC的中点，△EFC的面积为6cm2，则△ABC的面积为48cm2．
15．
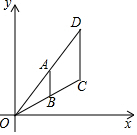如图，在平面直角坐标系中，点A在△ODC的OD边上，AB∥DC交OC于点B．若点A、B的坐标分别为（2，3）、（2，1），点C的横坐标为2m（m＞0），则点D的坐标为（ ）
如图，在平面直角坐标系中，点A在△ODC的OD边上，AB∥DC交OC于点B．若点A、B的坐标分别为（2，3）、（2，1），点C的横坐标为2m（m＞0），则点D的坐标为（ ）| A． | （2m，m） | B． | （2m，2m） | C． | （2m，3m） | D． | （2m，4m） |
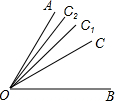如图，∠AOB=60°，OC是∠AOB的平分线，OC1是∠AOC的平分线，OC2是∠AOC1的平分线，…，OCn是∠AOCn-1的平分线，则∠AOCn=$\frac{1}{{2}^{n+1}}$×60°．