题目内容
7.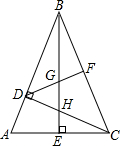 如图,在△ABC中∠ABC=45°,CD⊥BA,BE⊥AC,F为BC中点,∠ABE=∠CBE
如图,在△ABC中∠ABC=45°,CD⊥BA,BE⊥AC,F为BC中点,∠ABE=∠CBE(1)线段BH与线段AC相等吗?若相等给予证明,若不相等,请说明理由.
(2)若AC=12,BC=10,求BG的长.
分析 (1)根据三角形的内角和定理求出∠BCD=∠ABC,∠ABE=∠DCA,推出DB=CD,根据ASA证出△DBH≌△DCA即可;
(2)根据DB=DC和F为BC中点,得出DF垂直平分BC,推出BG=CG,根据BE⊥AC和∠ABE=∠CBE得出AE=CE,在Rt△CGE中,由勾股定理即可推出答案.
解答 解:(1)线段BH与线段AC相等.
证明:∵CD⊥AB,BE⊥AC,
∴∠BDH=∠BEC=∠CDA=90°,
∵∠ABC=45°,
∴∠BCD=180°-90°-45°=45°=∠ABC,
∴DB=DC,
∵∠BDH=∠BEC=∠CDA=90°,
∴∠A+∠ACD=90°,∠A+∠HBD=90°,
∴∠HBD=∠ACD,
∵在△DBH和△DCA中,
$\left\{\begin{array}{l}{∠BDH=∠CDA}\\{BD=CD}\\{∠HBD=∠ACD}\end{array}\right.$,
∴△DBH≌△DCA(ASA),
∴BH=AC;
(2)如图,连接CG,
由(1)知,DB=CD,
∵F为BC的中点,
∴DF垂直平分BC,
∴BG=CG,
∵∠ABE=∠CBE,BE⊥AC,
∴△ABE≌△CBE,
∴EC=EA=6,
∵Rt△BCE中,BC=10,CE=6,
∴BE=8,
设BG=CG=x,则GE=8-x,
∴Rt△CEH中,62+(8-x)2=x2,
∴x=$\frac{25}{4}$,
∴BG=$\frac{25}{4}$.
点评 本题考查了勾股定理,等腰三角形性质,全等三角形的性质和判定,线段的垂直平分线的性质的应用,注意:线段垂直平分线上的点到线段两端的距离相等,等腰三角形具有三线合一的性质.

练习册系列答案
相关题目
19.下列说法中,正确的是( )
| A. | 为检测市场上正在销售的酸奶质量,应该采用全面调查的方式 | |
| B. | 在连续5次的数学测试中,两名同学的平均分相同,方差较大的同学数学成绩更稳定 | |
| C. | 小强班上有3个同学都是16岁,因此小强认为他们班学生年龄的众数是16岁 | |
| D. | 给定一组数据,则这组数据的中位数一定只有一个 |
15.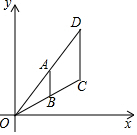 如图,在平面直角坐标系中,点A在△ODC的OD边上,AB∥DC交OC于点B.若点A、B的坐标分别为(2,3)、(2,1),点C的横坐标为2m(m>0),则点D的坐标为( )
如图,在平面直角坐标系中,点A在△ODC的OD边上,AB∥DC交OC于点B.若点A、B的坐标分别为(2,3)、(2,1),点C的横坐标为2m(m>0),则点D的坐标为( )
 如图,在平面直角坐标系中,点A在△ODC的OD边上,AB∥DC交OC于点B.若点A、B的坐标分别为(2,3)、(2,1),点C的横坐标为2m(m>0),则点D的坐标为( )
如图,在平面直角坐标系中,点A在△ODC的OD边上,AB∥DC交OC于点B.若点A、B的坐标分别为(2,3)、(2,1),点C的横坐标为2m(m>0),则点D的坐标为( )| A. | (2m,m) | B. | (2m,2m) | C. | (2m,3m) | D. | (2m,4m) |
16. 数a、b在数轴上的位置如图,则下列结论正确的是( )
数a、b在数轴上的位置如图,则下列结论正确的是( )
 数a、b在数轴上的位置如图,则下列结论正确的是( )
数a、b在数轴上的位置如图,则下列结论正确的是( )| A. | a<0 | B. | a>1 | C. | b<-1 | D. | b>-1 |

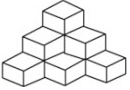 把若干个棱长为a的立方体摆成如图形状:从上向下数,摆一层有1个立方体,摆二层共有4个立方体,摆三层共有10个立方体,那么摆五层共有35个立方体.
把若干个棱长为a的立方体摆成如图形状:从上向下数,摆一层有1个立方体,摆二层共有4个立方体,摆三层共有10个立方体,那么摆五层共有35个立方体.