题目内容
14.观察下列各式,发现规律:$\sqrt{1+\frac{1}{3}}$=2$\sqrt{\frac{1}{3}}$;$\sqrt{2+\frac{1}{4}}$=3$\sqrt{\frac{1}{4}}$;$\sqrt{3+\frac{1}{5}}$=4$\sqrt{\frac{1}{5}}$;…(1)填空:$\sqrt{4+\frac{1}{6}}$=5$\sqrt{\frac{1}{6}}$,$\sqrt{5+\frac{1}{7}}$=6$\sqrt{\frac{1}{7}}$;
(2)计算(写出计算过程):$\sqrt{2015+\frac{1}{2017}}$;
(3)请用含自然数n(n≥1)的代数式把你所发现的规律表示出来.
分析 (1)根据等式的变化,再写出后面两个等式即可;
(2)通分后再开平方即可得出结论;
(3)根据等式的变化找出变化规律“$\sqrt{n+\frac{1}{n+2}}$=(n+1)$\sqrt{\frac{1}{n+2}}$(n≥1)”,此题得解.
解答 解:(1)∵$\sqrt{1+\frac{1}{3}}$=2$\sqrt{\frac{1}{3}}$;$\sqrt{2+\frac{1}{4}}$=3$\sqrt{\frac{1}{4}}$;$\sqrt{3+\frac{1}{5}}$=4$\sqrt{\frac{1}{5}}$;
∴$\sqrt{4+\frac{1}{6}}$=5$\sqrt{\frac{1}{6}}$,$\sqrt{5+\frac{1}{7}}$=6$\sqrt{\frac{1}{7}}$.
故答案为:5$\sqrt{\frac{1}{6}}$;6$\sqrt{\frac{1}{7}}$.
(2)$\sqrt{2015+\frac{1}{2017}}$=$\sqrt{\frac{2015×2017+1}{2017}}$=$\sqrt{\frac{4064256}{2017}}$=2016$\sqrt{\frac{1}{2017}}$.
(3)观察,发现规律:$\sqrt{1+\frac{1}{3}}$=2$\sqrt{\frac{1}{3}}$;$\sqrt{2+\frac{1}{4}}$=3$\sqrt{\frac{1}{4}}$;$\sqrt{3+\frac{1}{5}}$=4$\sqrt{\frac{1}{5}}$;…,
∴$\sqrt{n+\frac{1}{n+2}}$=(n+1)$\sqrt{\frac{1}{n+2}}$(n≥1).
点评 本题考查了实数以及规律型中数字的变化类,根据等式的变化找出变化规律是解题的关键.

 名校课堂系列答案
名校课堂系列答案| A. | (x-1)-2(2+3x)=13 | B. | (x-1)+2(2x+3)=1 | C. | 3(x-1)+2(2+3x)=6 | D. | 3(x-1)-2(2x+3)=6 |
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{1}{4}$ |
| A. | 为检测市场上正在销售的酸奶质量,应该采用全面调查的方式 | |
| B. | 在连续5次的数学测试中,两名同学的平均分相同,方差较大的同学数学成绩更稳定 | |
| C. | 小强班上有3个同学都是16岁,因此小强认为他们班学生年龄的众数是16岁 | |
| D. | 给定一组数据,则这组数据的中位数一定只有一个 |
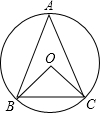 如图所示,△ABC内接于⊙O,AB=AC,∠BOC=120°.求$\widehat{AB}$和$\widehat{AC}$的度数.
如图所示,△ABC内接于⊙O,AB=AC,∠BOC=120°.求$\widehat{AB}$和$\widehat{AC}$的度数.
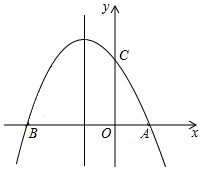 如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-1,且抛物线经过A(1,0),C(0,3)两点,与x轴相交于点B.
如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-1,且抛物线经过A(1,0),C(0,3)两点,与x轴相交于点B.