题目内容
5.已知关于x的一元二次方程(k-1)x2-(2k-3)x+k=0有实数根.(1)求k的取值范围;
(2)若x1、x2是方程的两实数根,且x${\;}_{1}^{2}$+x${\;}_{2}^{2}$=9,求k的值.
分析 (1)根据△≥0,解不等式即可解决问题,注意k≠1.
(2)列出方程即可解决问题,注意k的取值范围.
解答 解:(1)∵关于x的一元二次方程(k-1)x2-(2k-3)x+k=0有实数根,
∴△≥0,
∴4k2-12k+9-4k2+4k≥O,
∴k≤$\frac{9}{8}$,
∵k≠1,
∴k的取值范围为k≤$\frac{9}{8}$且k≠1.
(2)∵x1+x2=$\frac{2k-3}{k-1}$,x1x2=$\frac{k}{k-1}$,
∴($\frac{2k-3}{k-1}$)2-$\frac{2k}{k-1}$=9,
解得k=0或$\frac{8}{7}$,
∵的取值范围为k≤$\frac{9}{8}$且k≠1
∴k=0.
点评 本题考查根与系数关系,根的判别式等知识,解题的关键是灵活应用这些知识解决问题,学会把问题转化为方程解决,属于中考常考题型.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目
20.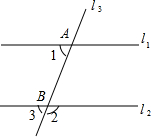 如图,直线l1∥l2,直线l3与l1,l2分别交于A,B两点,若∠1=65°,则∠2=( )
如图,直线l1∥l2,直线l3与l1,l2分别交于A,B两点,若∠1=65°,则∠2=( )
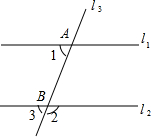 如图,直线l1∥l2,直线l3与l1,l2分别交于A,B两点,若∠1=65°,则∠2=( )
如图,直线l1∥l2,直线l3与l1,l2分别交于A,B两点,若∠1=65°,则∠2=( )| A. | 65° | B. | 75° | C. | 115° | D. | 125° |