题目内容
5.若$\left\{\begin{array}{l}{{a}_{1}x+{b}_{1}y={c}_{1}}\\{{a}_{2}x+{b}_{2}y={c}_{2}}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=3}\\{y=4}\end{array}\right.$,则$\left\{\begin{array}{l}{3{a}_{1}(x-1)+{b}_{1}(y+3)={c}_{1}}\\{3{a}_{2}(x-1)+{b}_{2}(y+3)={c}_{2}}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=4}\\{y=1}\end{array}\right.$.分析 根据已知得出方程组$\left\{\begin{array}{l}{x-1=3}\\{y+3=4}\end{array}\right.$,求出方程组的解即可.
解答 解:∵$\left\{\begin{array}{l}{{a}_{1}x+{b}_{1}y={c}_{1}}\\{{a}_{2}x+{b}_{2}y={c}_{2}}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=3}\\{y=4}\end{array}\right.$,
∴$\left\{\begin{array}{l}{x-1=3}\\{y+3=4}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=4}\\{y=1}\end{array}\right.$,
即$\left\{\begin{array}{l}{3{a}_{1}(x-1)+{b}_{1}(y+3)={c}_{1}}\\{3{a}_{2}(x-1)+{b}_{2}(y+3)={c}_{2}}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=4}\\{y=1}\end{array}\right.$,
故答案为:$\left\{\begin{array}{l}{x=4}\\{y=1}\end{array}\right.$.
点评 本题考查了二元一次方程组的解和解二元一次方程组,能根据题意得出关于x、y的方程组是解此题的关键.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
2.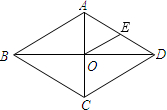 如图,菱形ABCD的对角线AC、BD相交于点O,E是AD的中点,连接OE,若OE=3,则菱形的周长是( )
如图,菱形ABCD的对角线AC、BD相交于点O,E是AD的中点,连接OE,若OE=3,则菱形的周长是( )
 如图,菱形ABCD的对角线AC、BD相交于点O,E是AD的中点,连接OE,若OE=3,则菱形的周长是( )
如图,菱形ABCD的对角线AC、BD相交于点O,E是AD的中点,连接OE,若OE=3,则菱形的周长是( )| A. | 6 | B. | 12 | C. | 18 | D. | 24 |
3.下列实数中,是无理数的为( )
| A. | -2 | B. | 0.101001 | C. | $\frac{1}{3}$ | D. | $\sqrt{5}$ |
20.估计$\sqrt{21}$的运算结果应在哪两个连续整数之间( )
| A. | 2和3 | B. | 3和4 | C. | 4和5 | D. | 5和6 |
7.下列实数是无理数的是( )
| A. | $\sqrt{4}$ | B. | $\frac{2}{3}$ | C. | -$\sqrt{5}$ | D. | 0 |
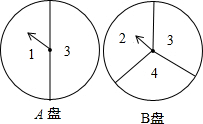 甲乙两同学玩转盘游戏时,把质地相同的两个盘A、B分别平均分成2份和3份,并在每一份内标有数字如图,游戏规则;甲乙两同学分别转动AB两个转盘,当转盘停止后,指针所在区或的数字之和为偶数时甲胜;数字之和为奇数时乙胜,若指针恰好在分割线上,则需要重新转动转盘.
甲乙两同学玩转盘游戏时,把质地相同的两个盘A、B分别平均分成2份和3份,并在每一份内标有数字如图,游戏规则;甲乙两同学分别转动AB两个转盘,当转盘停止后,指针所在区或的数字之和为偶数时甲胜;数字之和为奇数时乙胜,若指针恰好在分割线上,则需要重新转动转盘.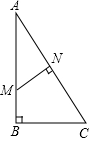 如图,在 Rt△ABC中,∠B=90°,AB=8,BC=4,AC的垂直平分线交AB于点M,交AC于N,则BM的值为3.
如图,在 Rt△ABC中,∠B=90°,AB=8,BC=4,AC的垂直平分线交AB于点M,交AC于N,则BM的值为3.