题目内容

2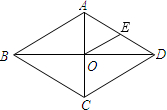．如图，菱形ABCD的对角线AC、BD相交于点O，E是AD的中点，连接OE，若OE=3，则菱形的周长是（　　）
A．6B．12C．18D．24

分析 由菱形的性质可得出AC⊥BD，AB=BC=CD=DA，再根据直角三角形斜边上的中线等于斜边的一半得出AD的长，结合菱形的周长公式即可得出结论．

解答 解：∵四边形ABCD为菱形，
∴AC⊥BD，AB=BC=CD=DA，
∴△AOD为直角三角形．
∵OE=3，且点E为线段AD的中点，
∴AD=2OE=6．
C菱形ABCD=4AD=4×6=24．
故选：D．

点评 本题考查了菱形的性质以及直角三角形的性质，解题的关键是求出AD=6．本题属于基础题，难度不大．

练习册系列答案
相关题目
12．用配方法解方程2x2-6x-1=0时，需要先将此方程化成形如（x+m）2=n（n≥0）的形式，则下列配方法正确的是（　　）
A．（x-3）2=$\frac{1}{2}$B．（x-$\frac{3}{2}$）2=$\frac{1}{2}$C．（x-$\frac{3}{2}$）2=2D．（x-$\frac{3}{2}$）2=$\frac{11}{4}$
13．下列因式分解正确的是（　　）
A．x3-x=x（x-1）B．x2+6x+9=（x+3）2
C．（2x+3y）（2x-3y）=4x2-9y2D．x2-y2=（x-y）2
10．已知小鹏家五月份总支出共计3600元，用扇形统计图表示时，教育的支出所在的扇形的圆心角是108度，那么其中用于教育上的支出是1080元．
17．要得到函数y=2x+3的图象，只需将函数y=2x的图象（　　）
A．向左平移3个单位B．向右平移3个单位C．向上平移3个单位D．向下平移3个单位
7．解方程组
（1）$\left\{\begin{array}{l}{x-y=1}\\{2x+y=5}\end{array}\right.$．
（2）$\left\{\begin{array}{l}{5x-1＞3x+3}\\{\frac{x}{2}-1≤7-\frac{3x}{2}}\end{array}\right.$．
14．为传播奥运知识，小刚就本班学生对奥运知识的了解程度进行了一次调查统计：A：熟悉，B：了解较多，C：一般了解．图1和图2是他采集数据后，绘制的两幅不完整的统计图，请你根据图中提供的信息解答以下问题：
（1）求该班共有多少名学生；
（2）在条形图中，将表示“一般了解”的部分补充完整；
（3）在扇形统计图中，计算出“了解较多”部分所对应的圆心角的度数；
（4）如果全年级共1000名同学，请你估算全年级对奥运知识“了解较多”的学生人数．
11．在△ABC中，三边长为9、10、x，则x的取值范围是（　　）
A．1≤x＜19B．1＜x≤19C．1＜x＜19D．1≤x≤19
5．若$\left\{\begin{array}{l}{{a}_{1}x+{b}_{1}y={c}_{1}}\\{{a}_{2}x+{b}_{2}y={c}_{2}}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=3}\\{y=4}\end{array}\right.$，则$\left\{\begin{array}{l}{3{a}_{1}（x-1）+{b}_{1}（y+3）={c}_{1}}\\{3{a}_{2}（x-1）+{b}_{2}（y+3）={c}_{2}}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=4}\\{y=1}\end{array}\right.$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网