题目内容
2.请先观察下列算式,再填空:32-12=8×1,52-32=8×2,72-52=8×3,92-72=8×4,…,通过观察归纳,写出反映这种规律的一般结论:(2n+1)2-(2n-1)2=8n.分析 结合题意可知,题目中等式左边的被减数和减数的底数都是连续的奇数的平方差,等式的右边是8的倍数,第一个式子是8的1倍,第二个式子是8的2倍,第三个式子是8的3倍,依此得出规律.
解答 解:由题意,可得第n个式子为(2n+1)2-(2n-1)2=8n.
故答案为(2n+1)2-(2n-1)2=8n.
点评 此题考查了规律型:数字的变化,得出两个连续奇数的平方差是8的倍数是解本题的关键.

练习册系列答案
相关题目
11.下列说法中正确的个数有( )
①有一个角为60°的等腰三角形是等边三角形;
②三边长为$\sqrt{14}$,$\sqrt{5}$,3的三角形为直角三角形;
③等腰三角形的两条边长为2,4,则等腰三角形的周长为10或8;
④一边上的中线等于这边长的一半的三角形是等腰直角三角形.
①有一个角为60°的等腰三角形是等边三角形;
②三边长为$\sqrt{14}$,$\sqrt{5}$,3的三角形为直角三角形;
③等腰三角形的两条边长为2,4,则等腰三角形的周长为10或8;
④一边上的中线等于这边长的一半的三角形是等腰直角三角形.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
12.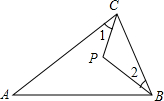 如图在等腰△ABC中,其中AB=AC,∠A=40°,P是△ABC内一点,且∠1=∠2,则∠BPC等于( )
如图在等腰△ABC中,其中AB=AC,∠A=40°,P是△ABC内一点,且∠1=∠2,则∠BPC等于( )
 如图在等腰△ABC中,其中AB=AC,∠A=40°,P是△ABC内一点,且∠1=∠2,则∠BPC等于( )
如图在等腰△ABC中,其中AB=AC,∠A=40°,P是△ABC内一点,且∠1=∠2,则∠BPC等于( )| A. | 110° | B. | 120° | C. | 130° | D. | 140° |
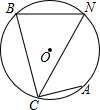 如图,⊙O是△BCN的外接圆,弦AC⊥BC,点N是$\widehat{AB}$的中点,∠BNC=60°,求$\frac{BN}{BC}$的值.
如图,⊙O是△BCN的外接圆,弦AC⊥BC,点N是$\widehat{AB}$的中点,∠BNC=60°,求$\frac{BN}{BC}$的值.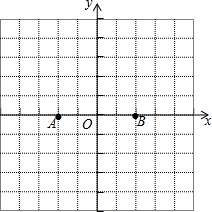 如图,在平面直角坐标系中,已知点A(-2,0),B(2,0).
如图,在平面直角坐标系中,已知点A(-2,0),B(2,0).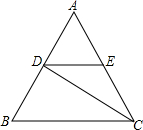 如图,△ABC是等边三角形,CD是∠ACB的平分线,过点D作BC的平行线交AC于点E,已知△ABC的边长为4,则EC的边长是2.
如图,△ABC是等边三角形,CD是∠ACB的平分线,过点D作BC的平行线交AC于点E,已知△ABC的边长为4,则EC的边长是2.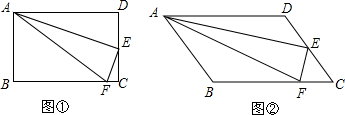
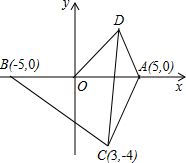 如图,在平面直角坐标系中,点A为(5,0),点B为(-5,0),点C为(3,-4),点D为第一象限上的一个动点,且OD=5.
如图,在平面直角坐标系中,点A为(5,0),点B为(-5,0),点C为(3,-4),点D为第一象限上的一个动点,且OD=5.