题目内容
17．
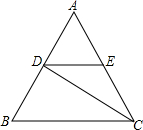如图，△ABC是等边三角形，CD是∠ACB的平分线，过点D作BC的平行线交AC于点E，已知△ABC的边长为4，则EC的边长是2．
分析 由△ABC是等边三角形，CD是∠ACB的平分线，利用三线合一的性质，可得AD=BD，又由DE∥BC，可得DE是△ABC的中位线，即可求得DE的长，易证得△DCE是等腰三角形，则可求得答案．
解答 解：∵△ABC是等边三角形，CD是∠ACB的平分线，
∴AD=BD，∠ACD=∠BCD，
∵DE∥BC，
∴DE=$\frac{1}{2}$BC=$\frac{1}{2}$×4=2，∠EDC=∠BCD，
∴∠EDC=∠ACD，
∴EC=DE=$\frac{1}{2}$×4=2．
故答案为2．
点评 本题考查了等边三角形的性质、等腰三角形的判定与性质以及三角形中位线的性质．注意由角平分线与平行线，可构造等腰三角形．
练习册系列答案
相关题目
如图，已知抛物线m经过原点O，与x轴交于点A（-3，0），P为抛物线的顶点将抛物线m平移后得到抛物线y=（x+$\frac{3}{2}$）2，其中点A，P，O的对应点分别为A′，P′，O′，连接AA′，则图中阴影部分的面积为$\frac{27}{4}$．
8．
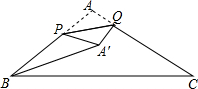如图，在△ABC中，AB=AC=2，∠ABC=30°，点P、Q分别在边AB、AC上，将△APQ沿PQ翻折，点A落到点A′处，则线段BA′长度的最小值是（ ）
如图，在△ABC中，AB=AC=2，∠ABC=30°，点P、Q分别在边AB、AC上，将△APQ沿PQ翻折，点A落到点A′处，则线段BA′长度的最小值是（ ）| A． | 2$\sqrt{3}$-2 | B． | 2 | C． | $\sqrt{3}$ | D． | $\sqrt{2}$ |
5．如图，给出线段a、h，作等腰三角形ABC，使AB=AC=a，BC边上的高AD=h．张红的作法是：（1）作线段AD=h；（2）作线段AD的垂线MN；（3）以点A为圆心，a为半径作弧，与MN分别交于点B、C；（4）连接AB、AC、△ABC为所求作的等腰三角形．上述作法的四个步骤中，你认为有错误的一步是（ ）
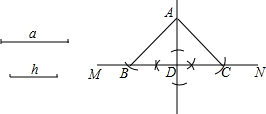
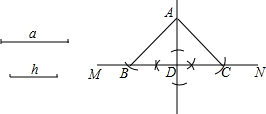
| A． | （1） | B． | （2） | C． | （3） | D． | （4） |
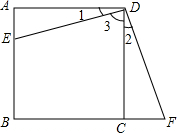如图所示，点E是矩形ABCD的边AB上任意一点，过点D作DF⊥DE交BC的延长线于点F，DE=DF．求证：矩形ABCD是正方形．
如图是“明清影视城”的圆弧形门，这个圆弧形门所在的圆与水平地面是相切的，AB=CD=20cm，BD=200cm，且AB，CD与水平地面都是垂直的．则这个圆弧形门的最高点离地面的高度是520 cm．
已知：直线y=-x-4分别交x、y轴于A、C两点，抛物线y=ax2+bx（a＞0）经过A、O两点，且顶点B的纵坐标为-2