题目内容
12.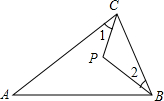 如图在等腰△ABC中,其中AB=AC,∠A=40°,P是△ABC内一点,且∠1=∠2,则∠BPC等于( )
如图在等腰△ABC中,其中AB=AC,∠A=40°,P是△ABC内一点,且∠1=∠2,则∠BPC等于( )| A. | 110° | B. | 120° | C. | 130° | D. | 140° |
分析 根据∠A=40°的条件,求出∠ACB+∠ABC的度数,再根据∠ABC=∠ACB,∠1=∠2,求出∠PBA=∠PCB,于是可求出∠1+∠ABP=∠PCB+∠2,然后根据三角形的内角和定理求出∠BPC的度数.
解答 解:∵∠A=40°,
∴∠ACB+∠ABC=180°-40°=140°,
又∵∠ABC=∠ACB,∠1=∠2,
∴∠PBA=∠PCB,
∴∠1+∠ABP=∠PCB+∠2=140°×$\frac{1}{2}$=70°,
∴∠BPC=180°-70°=110°.
故选A.
点评 此题不仅考查了三角形的内角和定理,还考查了同学们的整体思维能力,有一定难度.

练习册系列答案
相关题目
20.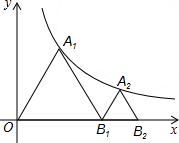 如图,点A1,A2依次在y=$\frac{4\sqrt{3}}{x}$(x>0)的图象上,点B1,B2依次在x轴的正半轴上,若△A1OB1,△A2B1B2均为等边三角形,则点B2的坐标为( )
如图,点A1,A2依次在y=$\frac{4\sqrt{3}}{x}$(x>0)的图象上,点B1,B2依次在x轴的正半轴上,若△A1OB1,△A2B1B2均为等边三角形,则点B2的坐标为( )
 如图,点A1,A2依次在y=$\frac{4\sqrt{3}}{x}$(x>0)的图象上,点B1,B2依次在x轴的正半轴上,若△A1OB1,△A2B1B2均为等边三角形,则点B2的坐标为( )
如图,点A1,A2依次在y=$\frac{4\sqrt{3}}{x}$(x>0)的图象上,点B1,B2依次在x轴的正半轴上,若△A1OB1,△A2B1B2均为等边三角形,则点B2的坐标为( )| A. | (4,0) | B. | (4$\sqrt{2}$,0) | C. | (6,0) | D. | (6$\sqrt{2}$,0) |
4.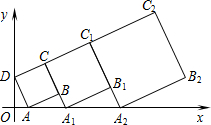 在平面直角坐标系中,第一个正方形ABCD的位置如图所示,点A的坐标为(2,0),点D的坐标为(0,4).延长CB交x轴于点A1,作第二个正方形A1B1C1C;延长C1B1交x轴于点A2,作第三个正方形A2B2C2C1,…,按这样的规律进行下去,第2016个正方形的面积为( )
在平面直角坐标系中,第一个正方形ABCD的位置如图所示,点A的坐标为(2,0),点D的坐标为(0,4).延长CB交x轴于点A1,作第二个正方形A1B1C1C;延长C1B1交x轴于点A2,作第三个正方形A2B2C2C1,…,按这样的规律进行下去,第2016个正方形的面积为( )
 在平面直角坐标系中,第一个正方形ABCD的位置如图所示,点A的坐标为(2,0),点D的坐标为(0,4).延长CB交x轴于点A1,作第二个正方形A1B1C1C;延长C1B1交x轴于点A2,作第三个正方形A2B2C2C1,…,按这样的规律进行下去,第2016个正方形的面积为( )
在平面直角坐标系中,第一个正方形ABCD的位置如图所示,点A的坐标为(2,0),点D的坐标为(0,4).延长CB交x轴于点A1,作第二个正方形A1B1C1C;延长C1B1交x轴于点A2,作第三个正方形A2B2C2C1,…,按这样的规律进行下去,第2016个正方形的面积为( )| A. | 20×($\frac{3}{2}$)4030 | B. | 20×($\frac{3}{2}$)4032 | C. | 20×($\frac{3}{2}$)2016 | D. | 20×($\frac{3}{2}$)2015 |
1.学习了数据的收集、整理与表示之后,某小组同学对本校“自主选修活动课”比较感兴趣,他们以问卷的形式随机调查了40名学生的选课情况(每人只能选一项),并统计如下:
(1)请选择一种统计图将上表中的结果表示出来;
(2)该校共有500名学生,请估计选修篮球课的人数;并说明你估计的理由;
(3)谈谈你对该校“自主选修活动课”的科目设置有哪些建议?
| 科目 | 篮球 | 围棋 | 剪纸 | 舞台剧 | 茶艺 | 交谊舞 | 其它课 |
| 计数 | 正正 | 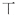 |  | 正 |  | 正一 | 正一 |
(2)该校共有500名学生,请估计选修篮球课的人数;并说明你估计的理由;
(3)谈谈你对该校“自主选修活动课”的科目设置有哪些建议?
 已知:直线y=-x-4分别交x、y轴于A、C两点,抛物线y=ax2+bx(a>0)经过A、O两点,且顶点B的纵坐标为-2
已知:直线y=-x-4分别交x、y轴于A、C两点,抛物线y=ax2+bx(a>0)经过A、O两点,且顶点B的纵坐标为-2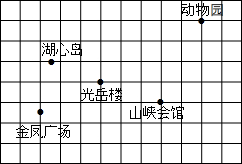 如图是某市市区几个旅游景点的示意图(图中每个小正方形的边长都为1个单位长度).建立适当的平面直角坐标系,使光岳楼的坐标为(-1,0),并用坐标表示下列景点的位置.
如图是某市市区几个旅游景点的示意图(图中每个小正方形的边长都为1个单位长度).建立适当的平面直角坐标系,使光岳楼的坐标为(-1,0),并用坐标表示下列景点的位置. 已知:如图,在?ABCD中,O为对角线BD的中点,过点O的直线EF分别交AD,BC于E,F两点,连结BE,DF.求证:△DOE≌△BOF.
已知:如图,在?ABCD中,O为对角线BD的中点,过点O的直线EF分别交AD,BC于E,F两点,连结BE,DF.求证:△DOE≌△BOF.