题目内容
13.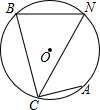 如图,⊙O是△BCN的外接圆,弦AC⊥BC,点N是$\widehat{AB}$的中点,∠BNC=60°,求$\frac{BN}{BC}$的值.
如图,⊙O是△BCN的外接圆,弦AC⊥BC,点N是$\widehat{AB}$的中点,∠BNC=60°,求$\frac{BN}{BC}$的值.
分析 连接AB、AN,先证明△ABN是以AB为底边的等腰直角三角形,从而得到BN=$\frac{\sqrt{2}}{2}$AB ①,再求出BC=$\frac{\sqrt{3}}{2}$AB ②,利用①÷②即可解答.
解答 解:如图,连接AB、AN,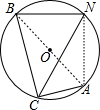
∵弦AC⊥弦BC,
∴弦AB是⊙O的直径,
∴∠ANB=90°,
∵点N是$\widehat{AB}$的中点,
∴AN=BN,
∴△ABN是以AB为底边的等腰直角三角形,
∴BN=$\frac{\sqrt{2}}{2}$AB ①,
∵∠BNC=60°,
∴∠BAC=60°,
又∠ACB=90°,
∴BC=$\frac{\sqrt{3}}{2}$AB ②
①÷②,得:
$\frac{BN}{BC}=\frac{\frac{\sqrt{2}}{2}}{\frac{\sqrt{3}}{2}}=\frac{\sqrt{6}}{3}$.
点评 本题考查了等腰直角三角形的判定、性质,解决本题的关键是表示出BN,BC与AB的数量关系.

练习册系列答案
相关题目
8.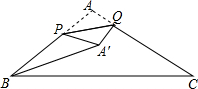 如图,在△ABC中,AB=AC=2,∠ABC=30°,点P、Q分别在边AB、AC上,将△APQ沿PQ翻折,点A落到点A′处,则线段BA′长度的最小值是( )
如图,在△ABC中,AB=AC=2,∠ABC=30°,点P、Q分别在边AB、AC上,将△APQ沿PQ翻折,点A落到点A′处,则线段BA′长度的最小值是( )
 如图,在△ABC中,AB=AC=2,∠ABC=30°,点P、Q分别在边AB、AC上,将△APQ沿PQ翻折,点A落到点A′处,则线段BA′长度的最小值是( )
如图,在△ABC中,AB=AC=2,∠ABC=30°,点P、Q分别在边AB、AC上,将△APQ沿PQ翻折,点A落到点A′处,则线段BA′长度的最小值是( )| A. | 2$\sqrt{3}$-2 | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
 如图,已知AB是⊙O的直径,AD切⊙O于点A,点C是$\widehat{EB}$的中点,则下列结论成立的是①②③(将正确番号填入)
如图,已知AB是⊙O的直径,AD切⊙O于点A,点C是$\widehat{EB}$的中点,则下列结论成立的是①②③(将正确番号填入) 在△ABC中,AB=14,AE=12,BD=7,BC=28,且∠BAD=∠EAC.
在△ABC中,AB=14,AE=12,BD=7,BC=28,且∠BAD=∠EAC.