题目内容
13.甲、乙两同学一起解关于x,y的方程组$\left\{\begin{array}{l}{ax+y=10}\\{x+by=7}\end{array}\right.$时,由于粗心,甲看错了方程组中的a,得到方程组的解为$\left\{\begin{array}{l}{x=6}\\{y=1}\end{array}\right.$:乙看错了方程组中的b,得到方程组的解为$\left\{\begin{array}{l}{x=-1}\\{y=12}\end{array}\right.$,问原方程组的解为多少?分析 把甲得到的解代入第二个方程,把乙得到的解代入第一个方程,然后求解可得a、b的值,把a、b的值代入方程组,然后利用加减消元法求解即可.
解答 解:由题意得$\left\{\begin{array}{l}{6+b=7}\\{-a+12=10}\end{array}\right.$,
解得:a=2,b=1,
将a=2、b=1代入原方程组得:$\left\{\begin{array}{l}{2x+y=10}&{①}\\{x+y=7}&{②}\end{array}\right.$,
①-②,得:x=3,
将x=3代入①,得:6+y=10,解得:y=4,
故原方程组的解为:$\left\{\begin{array}{l}{x=3}\\{y=4}\end{array}\right.$.
点评 本题考查的是方程组的解及二元一次方程组的解法,方程组中未知数的系数较小时可用代入法,当未知数的系数相等或互为相反数时用加减消元法较简单.

练习册系列答案
相关题目
 如图所示,直线y=2x+4与x轴、y轴分别交于A,B两点,以OB为一边在y轴的右侧作等边三角形OBC,将点C向左平移到点C′,且C′恰在AB上,求CC′的长.
如图所示,直线y=2x+4与x轴、y轴分别交于A,B两点,以OB为一边在y轴的右侧作等边三角形OBC,将点C向左平移到点C′,且C′恰在AB上,求CC′的长. 如图,已知抛物线m经过原点O,与x轴交于点A(-3,0),P为抛物线的顶点将抛物线m平移后得到抛物线y=(x+$\frac{3}{2}$)2,其中点A,P,O的对应点分别为A′,P′,O′,连接AA′,则图中阴影部分的面积为$\frac{27}{4}$.
如图,已知抛物线m经过原点O,与x轴交于点A(-3,0),P为抛物线的顶点将抛物线m平移后得到抛物线y=(x+$\frac{3}{2}$)2,其中点A,P,O的对应点分别为A′,P′,O′,连接AA′,则图中阴影部分的面积为$\frac{27}{4}$.
 如图,已知AB是⊙O的直径,AD切⊙O于点A,点C是$\widehat{EB}$的中点,则下列结论成立的是①②③(将正确番号填入)
如图,已知AB是⊙O的直径,AD切⊙O于点A,点C是$\widehat{EB}$的中点,则下列结论成立的是①②③(将正确番号填入)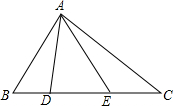 在△ABC中,AB=14,AE=12,BD=7,BC=28,且∠BAD=∠EAC.
在△ABC中,AB=14,AE=12,BD=7,BC=28,且∠BAD=∠EAC.