题目内容
10.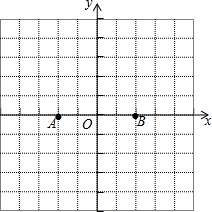 如图,在平面直角坐标系中,已知点A(-2,0),B(2,0).
如图,在平面直角坐标系中,已知点A(-2,0),B(2,0).(1)画出等边三角形ABC(画出一个即可);
(2)写出(1)中画出的△ABC的顶点C的坐标.
分析 (1)分别以A,B为圆心,以AB的长为半径画弧交y轴于C连接AC,BC,则△ABC即为所求;
(2)根据A(-2,0),B(2,0).得到AB=4,由△ABC是等边三角形,得到AC=BC=4,解直角三角形即可得到结论.
解答  解:(1)如图所示,
解:(1)如图所示,
(2)∵A(-2,0),B(2,0).
∴AB=4,
∵△ABC是等边三角形,
∴AC=BC=4,
∵A,B在x轴上,
∴C在y轴上,
∴OC=2$\sqrt{3}$,
∴C(0,2$\sqrt{3}$),或C(0,-2$\sqrt{3}$).
点评 本题考查了等边三角形的性质,坐标与图形的性质,基本作图,熟练掌握基本作图的方法是解题的关键.

练习册系列答案
相关题目
5.如图,给出线段a、h,作等腰三角形ABC,使AB=AC=a,BC边上的高AD=h.张红的作法是:(1)作线段AD=h;(2)作线段AD的垂线MN;(3)以点A为圆心,a为半径作弧,与MN分别交于点B、C;(4)连接AB、AC、△ABC为所求作的等腰三角形.上述作法的四个步骤中,你认为有错误的一步是( )
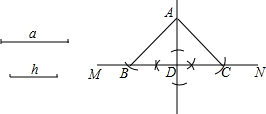
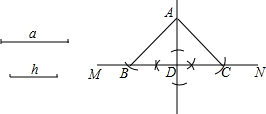
| A. | (1) | B. | (2) | C. | (3) | D. | (4) |
20.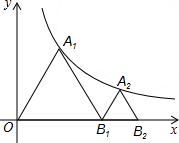 如图,点A1,A2依次在y=$\frac{4\sqrt{3}}{x}$(x>0)的图象上,点B1,B2依次在x轴的正半轴上,若△A1OB1,△A2B1B2均为等边三角形,则点B2的坐标为( )
如图,点A1,A2依次在y=$\frac{4\sqrt{3}}{x}$(x>0)的图象上,点B1,B2依次在x轴的正半轴上,若△A1OB1,△A2B1B2均为等边三角形,则点B2的坐标为( )
 如图,点A1,A2依次在y=$\frac{4\sqrt{3}}{x}$(x>0)的图象上,点B1,B2依次在x轴的正半轴上,若△A1OB1,△A2B1B2均为等边三角形,则点B2的坐标为( )
如图,点A1,A2依次在y=$\frac{4\sqrt{3}}{x}$(x>0)的图象上,点B1,B2依次在x轴的正半轴上,若△A1OB1,△A2B1B2均为等边三角形,则点B2的坐标为( )| A. | (4,0) | B. | (4$\sqrt{2}$,0) | C. | (6,0) | D. | (6$\sqrt{2}$,0) |
 如图所示,直线y=2x+4与x轴、y轴分别交于A,B两点,以OB为一边在y轴的右侧作等边三角形OBC,将点C向左平移到点C′,且C′恰在AB上,求CC′的长.
如图所示,直线y=2x+4与x轴、y轴分别交于A,B两点,以OB为一边在y轴的右侧作等边三角形OBC,将点C向左平移到点C′,且C′恰在AB上,求CC′的长.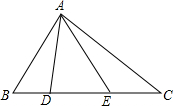 在△ABC中,AB=14,AE=12,BD=7,BC=28,且∠BAD=∠EAC.
在△ABC中,AB=14,AE=12,BD=7,BC=28,且∠BAD=∠EAC.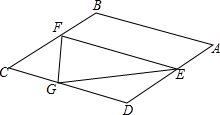 如图,在菱形ABCD中,AB=$\sqrt{3}$,∠B=120°,E是AD边上的一个动点(不与点A,D重合),EF∥AB交BC于点F,点G在CD上,DG=DE.
如图,在菱形ABCD中,AB=$\sqrt{3}$,∠B=120°,E是AD边上的一个动点(不与点A,D重合),EF∥AB交BC于点F,点G在CD上,DG=DE.